Расчёт деформируемых стержневых систем методом перемещений: Методические указания к индивидуальному расчётному заданию по курсу «Строительная механика», страница 11

         в) взаимозависимыми являются также деформации элементов при кинематических воздействиях – смещениях связей, в т.ч. и дополнительно введённых в расчётные узлы. 

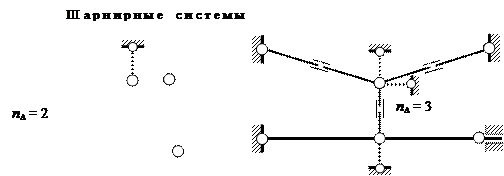
          На рис. 1.18 приведены некоторые характерные примеры построения основных систем – для рамы с неортогональными стержнями (рис. 1.18, а), комбинированной системы (рис. 1.18, б) и балки, имеющей упругие опоры ( рис. 1.18, в).

ЕА

а)                                                         б)

 

  

nq = nж.у. = 1

          

 

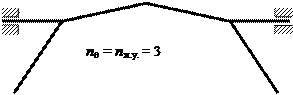                 в)

 

 

nk = 4

 

	Рис. 1.18

 

1.4. Канонические уравнения метода перемещений

14

         Канонические ( основные ) уравнения – главная часть мате-матической модели расчёта, формируемой с использованием     физической расчётной модели, роль которой играет основная система.

17

1.4.1. Сущность канонических уравнений

         Они получаются из условия эквивалентности напряжённо-деформированных состояний двух систем – заданной ( рассчитываемой )   и   основной  системы  МП,  если  к  обеим приложить заданные воздействия, а в ОСМП также задать дополнительным связям, введённым в расчётные узлы, смещения, равные действительным перемещениям Z₁ , …, Z_i , …, Z_n .  

         При выполнении указанного условия дополнительные   связи в ОСМП ( отсутствующие в заданной системе ) оказываются ненужными для обеспечения её равновесия, и, следовательно, их реакции становятся равными нулю: R₁ = 0, …, R_i = 0, …, R_n = 0

или                                     ,                           ( 1.10 )

где R _i – полная реакция i - й дополнительной связи в ОСМП  (со-

              вместно от заданных воздействий и смещений Z₁ , …, Z_n );

– число основных неизвестных ( n = n_k , если используется

              кинематически определимая основная система;  n < n_k  в

18

              случае выбора кинематически неопределимой ОСМП ).

         Уравнения ( 1.10 ),  выражающие  условие эквивалентности рассчитываемой системы и ОСМП, – статические. Принято говорить, что они отрицают полные реакции дополнительных связей в ОСМП.

         Далее имеются в виду только линейно деформируемые сис-темы, которые вследствие прямопропорциональной зависимо-сти между перемещениями ( деформациями ) и усилиями ( напря-жениями ) подчиняются  принципусуперпозиции  ( независимости воздействий ).  На основании этого принципа полную реакцию R_iможно представить как сумму составляющих – от заданных воз-

действий и от смещений связей в расчётных узлах^*) ( Z₁ , …, Z_n ):

                                            R _i  = R _iS + R _iZ ,                                ( 1.11 )

_______________________________________________________

^*) В дальнейшем введённые в расчётные узлы связи для краткости име-

    нуются иногда просто «связи» вместо «дополнительные связи».

где R_iS – реакция  i - й  связи в  ОСМП  от  заданного воздействия

               общего вида ( символ воздействия – S );   частными слу-

                чаями могут быть силовые воздействия – нагрузки (сим-

                вол F,  реакция  R_iF ), тепловые воздействия – изменения

                температуры ( символ t,  реакция R_it )  и  кинематические

                воздействия – смещения связей ( символ с, реакция R_iс );