Элементы сверхпроводящей электроники. Динамика кристаллической решетки. Магнитные квантовые эффекты в полупроводниках

Г Л А В А 18

ЭЛЕМЕНТЫ СВЕРХПРОВОДЯЩЕЙ ЭЛЕКТРОНИКИ

§18.1. Квантование магнитного потока

Если кольцо из сверхпроводника при высокой температуре поместить с магнитное поле, перпендикулярное плоскости кольца, затем охладить его до температуры ниже критической Т_с и выключить магнитное поле, то по закону Фарадея в кольце установится постоянный сверхпроводящий ток, а внутри кольца – постоянное “захваченное магнитное” поле (рис.18.1). Сверхпроводящее состояние характеризуется следующими особенностями:

1)  два электрона с противоположными спинами образуют куперовскую пару;

2)  поскольку куперовская пара является бозоном с нулевым спином, его энергия резко уменьшается на величину DE₀. Заметим, что для одного электрона, являющегося фермионом с полуцелым спином, уменьшение энергии невозможно в силу принципа Паули;

3)  энергии куперовской пары недостаточно для возбуждения фононов - квантов энергии, испускаемых атомами в результате их колебания. Спаренные электроны движутся в межатомном пространстве, не испытывая сопротивления со стороны атомов;

4) собственный магнитный момент спаренных электронов равен нулю. Сверхпроводник является идеальным диамаг-нетиком. Импульс двух спаренных электронов

,               (18.1)

где  - векторный потенциал, связанный с индукцией магнитного поля выражением .

Волновая функция имеет одинаковую амплитуду во всех точках сверхпроводника и отличается лишь фазой j(r)

.                                               (18.2)

где j(r) = ; k = 2p/l, - длина волны де-Бройля.

Применяя условие цикличности (однозначности y-функции), запишем

,                                      (18.3)

где n = 0, 1, 2, 3, ...

Из (18.3) следует, что изменение фазы при обходе по контуру l (рис.18.1) должно быть кратно 2p:

.                                            (18.4)

В каждой точке контура l скорость u = 0, поскольку сверхпроводящий ток существует только в тонком поверхностном слое кольца, а контур l расположен в центре его поперечного сечения. Поэтому из (18.1) и (18.4.) следует

.                                            (18.5)

Применяя теорему Стокса, получаем

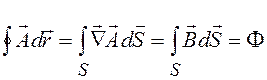,                                           (18.6)

где Ф - магнитный поток, пронизывающий сверхпроводящее кольцо.

Из (18.5) и (18.6) видно, что магнитный поток Ф квантован

Ф = nh / 2e = nФ₀,                                        (18.7)

где Ф₀ - квант магнитного потока, равный 2,07^.10^-15 Вб.

Выражение (18.7) легко получается из равенства кинетической энергии куперовской пары энергии магнитного поля, создаваемого этой парой,

mu² / 2 = ФI / 2 = Фen = Фeu / 2pr

Учитывая, что момент импульса пары относительно центра кольца квантован L_z = rр = n, получаем (18.7).

§ 18.2. Эффект Джозефсона. Переход Джозефсона

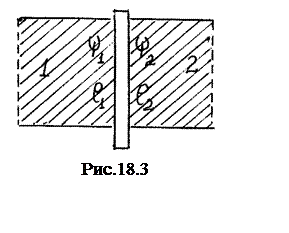Переход Джозефсона представляет собой две тонкие пленки из сверхпроводящего металла, разделенные очень тонким слоем диэлектрика (обычно очень тонкой пленкой окиси металла толщиной 10 Å) (рис.18.2). Эффект Джозефсона заключается в протекании сверхпроводящего тока через тонкий" слой диэлектрика, разделяющего два сверхпроводника. Свободные электроны проходят сквозь диэлектрик благодаря туннельному эффекту. Туннелирование куперовских пар сквозь диэлектрический барьер обусловлено перекрытием волновых функций этих пар, находящихся по обе стороны перехода. При отсутствии внешнего электрического и магнитного полей уравнения Шредингера для волновых функций спаренных электронов y₁ и y₂ имеют следующий вид:

;

(18.8)

;

Для одинаковых сверхпроводников основное состояние каждого из них одинаково, поэтому Е₁ = E₂. Энергетический параметр DE характеризует возможность туннелирования куперовской пары сквозь слой диэлектрика.

Теперь приложим внешнее напряжение U к переходу. Выберем для удобства Е₁ = 0, тогда Е₂ = 2eU и уравнения (18.8) преобразуются к виду:

;

 (18.9)

.

Вероятность нахождения куперовской пары по обе стороны перехода пропорциональна объемной r и поверхностной s плотностям свободных электронов на границе раздела сверхпроводник - диэлектрик, т.е. , либо . Коэффициент пропорциональности определяется из условия нормировки волновой функции. Для упрощения решения уравнений (18.9) волновые функции выбирают размерными в виде

,                ,                         (18.10)

где y₁ и y₂  - фазы волновых функций; r₁, r₂ - плотности электронов по обе стороны перехода. Если подставим (18.10) в (18.9), приравняем вещественные части вещественным, а мнимые - мнимым, обозначим y^* = y₁ - y₂   и разделим уравнения на общий множитель, то получим четыре уравнения:

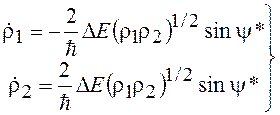;                               (18.11)

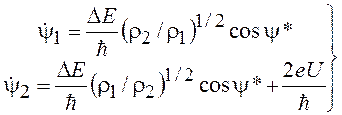.                               (18.12)

Уравнения (18.11) дают плотность тока через переход

j = j₀ sin y*.                                                 (18.13)

Из уравнения (18.12) при r₁ » r₂ получаем

.                                   (18.14)

Интегрируя (18.14), получаем зависимость разности фаз от мгновенного значения напряжения на переходе

.                                     (18.15)