Элементы сверхпроводящей электроники. Динамика кристаллической решетки. Магнитные квантовые эффекты в полупроводниках, страница 10

В области оптических частот вблизи плазменного и циклотронного резонансов изменение коэффициента отражения  пропорционально производной . Этим обусловлено усиление осцилляций Шубникова - де Гааза не только вблизи плазменного и циклотронного резонансов, но и вблизи края собственного поглощения. При удалении от областей резонансной зависимости коэффициентов отражения, пропускания и поглощения от частоты зондирующего излучения амплитуда осцилляций Шубникова - де Гааза убывает. Кроме этого, в оптическом эффекте Шубникова - де Гааза частота инфракрасного излучения во много раз превышает частоту столкновений электронов с атомами. Вследствие этого передача энергии зондирующего излучения свободным электронам, совершающим орбитальное движение в магнитном поле, происходит неэффективно. В таких случаях возникает необходимость уменьшения частоты зондирующего излучения для увеличения времени взаимодействия волны с электроном и следовательно, чувствительности метода, поскольку вероятность перехода электронов на уровни Ландау возрастает с увеличением периода волны.

Энергетический спектр двумерных носителей в системе GaAs/Al_xGa_1-xAs при В = 0 остается непрерывным в плоскости (xy), а в поперечном движении – дискретным в результате квантово-размерного эффекта.

Рассмотрим структуру энергетических уровней в гетеропереходе, образованных размерным квантованием в рамках приближения псевдотреугольной потенциальной ямы [24]. По мере удаления от границы раздела z = 0 (рис. 20.7) потенциал сначала линейно возрастает, а затем приближается к постоянному значению. Вклад инверсионного слоя в потенциал V(z) становится постоянным на расстоянии, превышающем в несколько раз величину среднего удаления электронов от границы раздела z_ср. Потенциальная энергия бесконечна при z < 0 и линейно возрастает при z > 0 в пределах инверсионного слоя                       

                                                                      (20.7)

где F – эффективное электрическое поле, определяемое по теореме Гаусса                        

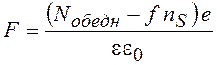                                               ,                                  (20.8)

f = 1/2  для среднего поля в инверсионном слое, f = 1 на границе раздела.

Заменой переменной

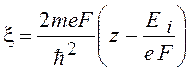                                                                     (20.9)

уравнение Шредингера в поле V(z) приводится к виду

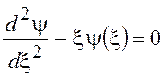                                                    .                                    (20.10)

Квантование энергии E_i возникает в силу граничного условия

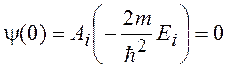                       .                                   (20.11)

Собственные значения E_i при больших i имеют следующий асимптотический вид

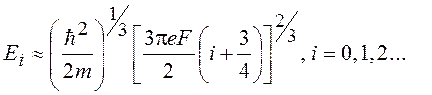                                 (20.12)

Точные собственные значения E_i получаются, если заменить 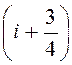 при  i = 0,1,2 соответственно числами 0.7587, 1.7540, 2.7575.

Для качественного исследования свойств инверсионного слоя решение уравнения (20.10) для нижней подзоны можно представить в приближенном виде

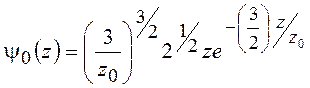                                        .                           (20.13)

где z₀ – среднее удаление электронов инверсионного слоя от поверхности полупроводника. Из (20.13) следует, что вероятность  максимальна при .

Поскольку поглощение высокочастотного электромагнитного поля в образце пропорционально вещественной части электропроводности, изменение коэффициента отражения в первом приближении пропорционально изменению электропроводности.

Два предельных случая >>1 и <<1 реализуются в оптическом и статическом эффектах Шубникова - де Гааза.