Элементы сверхпроводящей электроники. Динамика кристаллической решетки. Магнитные квантовые эффекты в полупроводниках, страница 14

Исследуя форму осцилляций Шубникова - де Гааза бесконтактным СВЧ – методом, можно заранее определить характер ожидаемых изменений холловского сопротивления ρ₁₂. Отсутствие глубоких провалов и острых максимумов осцилляций характеризует качество исследуемого 2D – слоя. В таких слоях не проявляются широкие ступени (плато) и скачкообразная зависимость ρ₁₂ от магнитного поля.

Осцилляции Шубникова - де Гааза периодичны по обратному магнитному полю В^-1 для образцов полупроводника, содержащих как объемный, так и двумерный вырожденный электронный газ. Чтобы отличить эти два случая, необходимо проводить измерения, поворачивая исследуемый образец, тем самым, изменяя угол наклона магнитного поля В к поверхности образца. В случае объемных образцов осцилляции не зависят от угла поворота образца. В случае двумерного (2D) – слоя на электронный газ действует только нормальная к двумерному слою, компонента магнитного поля B_n . Поэтому при повороте образца период осцилляций изменяется и, когда B_n = 0, осцилляции исчезают. Поведение осцилляций при отклонении магнитного поля от нормали к плоскости слоя является одним из ключевых тестов на двумерность исследуемых структур (гетеропереходов, содержащих 2D – слой, квантовых ям, образованных двумя гетеропереходами или сверхрешетками).

В отличие от контактных методов СВЧ – метод является неразрушающим методом и не требует абсолютных измерений, которые трудно выполнять при гелиевых температурах. Описанный метод позволяет определять концентрацию носителей с высокой точностью из относительных измерений, проводить измерения на объемных полупроводниках, пленочных структурах, на квантовых низкоразмерных системах.

§ 20.5 Бесконтактное определение подвижности и времени релаксации импульса носителей заряда в двумерных и тонкопленочных полупроводниковых структурах

Известные методы определения подвижности носителей заряда в двумерных (2D) системах и тонких пленках применимы для случаев полного и частичного заполнения образцом сечения волновода и основаны на определении проводимости s(w,B) образцов по измерениям коэффициента отражения R(w,B).

Автором с сотрудниками разработаны оптический [25] и СВЧ [26] способы и созданы устройства [27,28] для определения транспортных параметров объемных 3D и 2D полупроводниковых структур. Устройства позволяют измерять производные коэффициентов отражения ¶R/¶B и ¶²R/¶B² в зависимости от величины постоянного магнитного поля и определять концентрацию и подвижность носителей заряда в 3D и 2D полупроводниках при гелиевых и азотных температурах.

В этом параграфе подвижность m и время релаксации t носителей заряда определены по измеренным значениям магнитного поля В₁ и В₂, соответствующим максимумам первой и второй производных коэффициентов отражения СВЧ волны частотой wв области циклотронного резонанса при [29].

Теория метода определения подвижности и времени

релаксации импульса носителей заряда.

Коэффициент отражения СВЧ волны определяется известным выражением [30]

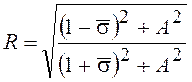,                                     (20.26)

где - нормированная проводимость активного слоя полупроводника;

, - концентрация носителей заряда в 2D-слое единичной площади;

d - толщина 2D-слоя;

Z_g - характеристическое сопротивление волновода;

A - нормированная реактивная проводимость СВЧ-цепи.

При настройке СВЧ-цепи на минимум сигнала в нулевом магнитном поле A=0. Тогда коэффициент отражения

.                                               (20.27)

Рассмотрим взаимодействие СВЧ-волны с образцом, помещенным в центральной части волновода в постоянное магнитное поле, направленное вдоль оси волновода. Образец повернут активным слоем к фронту падающей волны. Линейно поляризованную волну в случае геометрии Фарадея можно рассматривать как суперпозицию двух волн круговой поляризации [31]. При этом высокочастотная проводимость, возбужденная СВЧ-волной в образце, без учета распределения носителей по энергиям может быть представлена приближенным выражением