Элементы сверхпроводящей электроники. Динамика кристаллической решетки. Магнитные квантовые эффекты в полупроводниках, страница 8

В оптическом эффекте Шубникова – де Гааза измеряемой величиной является мощность поглощаемого, отражаемого и проходящего зондирующих излучений. Осцилляции мощности излучения и соответственно оптических коэффициентов происходят в результате упругого рассеяния электронов, имеющих энергию вблизи энергии Ферми E_F. При возрастании магнитного поля В энергетические интервалы между уровнями Ландау E_N возрастают и, когда уровень Ландау E_N пересекает уровень Ферми, электроны с уровня Ферми интенсивно переходят без изменения энергии на свободные состояния уровней Ландау E_N, E_N-1, E_N-2…, (рис.20.1). В отличие от статического эффекта Шубникова – де Гааза в высокочастотной проводимости участвуют все электроны, имеющие энергию меньше энергии Ферми E_F. Для наблюдения эффекта Шубникова – де Гааза необходимо, чтобы выполнялись условия (20.3) , из которых следует, что исследуемый образец должен быть вырожденным, а эксперимент необходимо выполнять при гелиевых температурах и сильных квантующих магнитных полях. Упругое рассеяние электронов при E_F = E_N происходит эффективно, если время релаксации свободного электрона больше периода обращения электрона по орбите . С другой стороны, упругое взаимодействие электромагнитной волны с электронами, имеющими энергию Ландау E_N, вызывает интенсивно переходы электронов с уровня Ферми на свободные локализованные состояния уровней Ландау. При этом необходимо, чтобы электрический вектор  электромагнитной волны был перпендикулярен вектору индукции магнитного поля . Для исключения межзонных эффектов энергия фотонов зондирующего излучения должна быть меньше ширины запрещенной зоны. В нашем случае для n-InSb λ>5.3 мкм.

Рассмотрим вывод рабочей формулы для определения концентрации с учетом влияния магнитного поля на энергию Ферми, непараболичности зоны проводимости n-InSb, спина электрона и температуры. Заметим, что без учета этих факторов обычно используют формулу (16.50) для контактного определения концентрации по осцилляциям магнитосопротивления

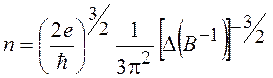                  .                                               (20.4)

Однако, применение (20.4) приводит к погрешности определения концентрации n при малых значениях номера уровня Ландау N.

Выражение для определения концентрации свободных носителей заряда по измеренным положениям максимумов осцилляций коэффициентов отражения и пропускания, либо поперечного магнитосопротивления имеет вид

                                                                          (20.5)

где                   

Коэффициент a_N при N<3 зависит от магнитного поля.

При   и 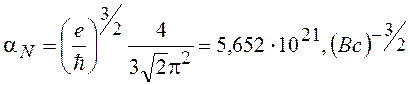, В – вольт, с - секунда.

Основной вклад в изменение коэффициента  дает влияние магнитного поля на энергию Ферми E_F. Расчет показывает, что при  этот вклад в увеличение α_min составляет меньше 0,5 %.

Из анализа условий наблюдения осцилляций Шубникова-де Гааза следует, что точность определения концентрации носителей зависит от точности измерения периода осцилляций интенсивности проходящего либо отраженного монохроматического поляризованного излучения.

На рис.20.3 приведена зависимость второй производной интенсивности излучения  от магнитного поля B для двух образцов n-InSb. По графикам рис. 20.3 определяются периоды осцилляций  и по расчетной формуле (20.5) вычисляется концентрация носителей заряда в исследуемых образцах.

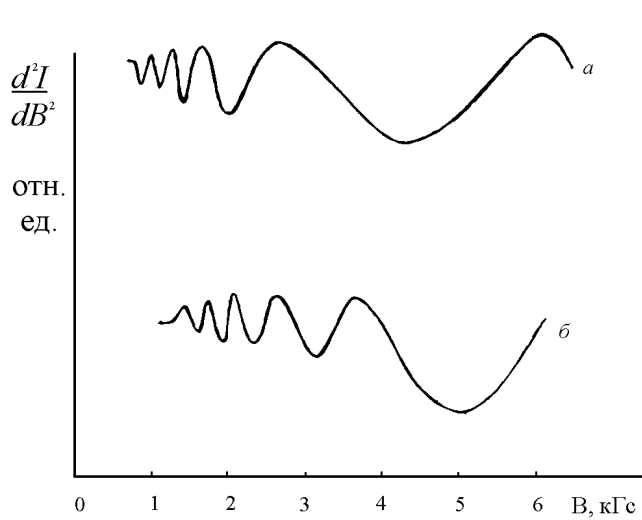
Рис. 20.3. Характерный вид осцилляций Шубникова де-Гааза. Зависимость второй производной интенсивности прошедшего излучения от магнитного поля для n – InSb. (кривая а n₁ = 2,20×10¹⁵ см^-3, кривая б n₂ = 5,21×10¹⁵ см^-3).

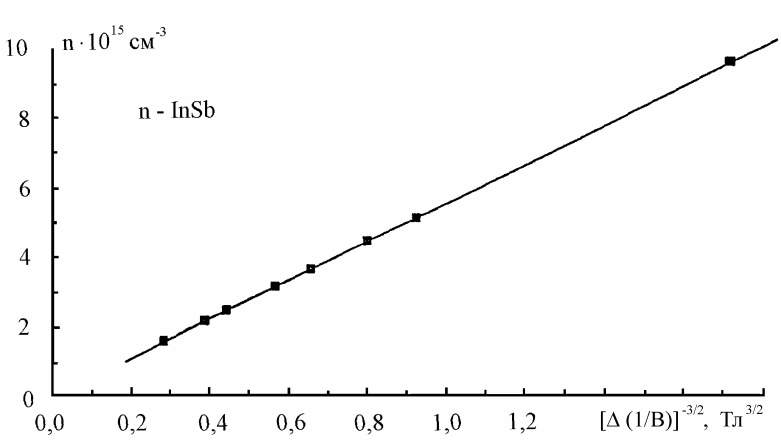
Рис. 20.4. Градуировочный график зависимости концентрации носителей заряда n_e от периода по обратному магнитному полю [D(I/B)]^-3/2, Тл^3/2.

Исследования образцов InSb n - типа с различными концентрациями свободных электронов показали, что зависимость концентрации носителей n, от  является линейной (рис.20.4). Погрешность измерений концентрации n в исследованных образцах составляет 0,5% и обусловлена точностью определения положения максимумов осцилляций пропускания либо отражения B_N и B_N+1.