Элементы сверхпроводящей электроники. Динамика кристаллической решетки. Магнитные квантовые эффекты в полупроводниках, страница 5

Число фононов зависит от интенсивности колебаний атомов, т.е. от температуры кристалла. Фонон не локализован в какой-либо точке кристалла, а является коллективным возбуждением атомов кристалла. Поскольку число фононов с одинаковой энергией не ограничено, принцип Паули не распространяется на фононы. Момент импульса фонона равен нулю, и фонон является бозоном с нулевым спином. В случае теплового равновесия среднее число фононов в одном квантовом состоянии определяется функцией Бозе - Эйнштейна

.                                 (19.45)

Другими словами, выражение (19.45) определяет среднее число фононов с энергией  в данном нормальном колебании или в ячейке фазового пространства h³.

§ 19.4. Энергия и теплоемкость трехмерной кристаллической решетки

В трехмерной решетке фононы распространяются по всем направлениям. Поскольку число атомов N велико, изменения k, p и w можно рассматривать как квазинепрерывные.

Определим плотность квантовых состояний (число нормальных колебаний или число упругих волн) с частотой w в изотропной кубической решетке, элементарная ячейка которой состоит из одного атома.

Как было показано для линейной атомной цепочки (9.13), волновое число принимает дискретные значения. Проекции импульсов фононов на оси координат в трехмерной решетке изменяются также дискретно:

; ; .        (19.46)

; ; .               (19.47)

Произведение изменений импульсов определяет объем элементарной ячейки пространства импульсов

.                                   (19.48)

При V = 1 объем ячейки фазового пространства равен h³. Плотность состояний с частотой w определяем известным способом [см. формулу (14.6)]

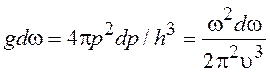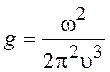;   ,                    (19.49)

где u - скорость распространения упругих волн (фононов) в кристалле .

Преобразуем (19.49) с учетом одной продольной и двух поперечных упругих волн одинаковой частоты. Другими словами, учтем три взаимно перпендикулярные поляризации фононов. Тогда плотность состояний с частотой w

,                                          (19.50)

где 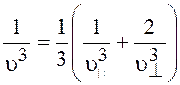; u_½½ и u_^ - скорости фононов с продольной и поперечной поляризациями.

Энергия единицы объема кристаллической решетки без учета нулевых колебаний равна произведению плотности всех состояний на энергию фононов в каждом состоянии

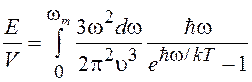.                                    (19.51)

Максимальное число состояний равно числу степеней свободы, другими словами, числу нормальных колебаний или числу упругих волн. Для единичного объема кристалла максимальная плотность состояний

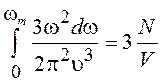.                                         (19.52)

Из  (19.52) определяем максимальную частоту

.                                                (19.53)

При низких температурах, когда kT << , верхний предел интегрирования в (19.51) можно принять равным бесконечности. Умножив и разделив (19.51) на  и перейдя к новой переменной , преобразуем (19.51)

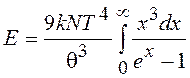,                                    (19.54)

где  - температура Дебая. Табличный интеграл равен p⁴/15.

Энергия моля кристалла в случае низких температур без учета нулевых колебаний и энергии электронов

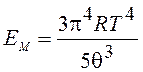,                                            (19.55)

где R = kN_A, N_A - число Авогадро.

Молярная теплоемкость кристаллической решетки (рис.19.5)-закон Дебая

C_V=dE_M/dT = 234R(T/q)³.                            (19.56)

При высоких температурах, когда , среднее число фононов в одном квантовом состоянии равно , а энергия, приходящаяся на одно состояние (на одно нормальное колебание), равна kT, число состояний для моля кристалла равно 3N_A. Энергия моля кристалла без учета энергии электронов

E_M =  3N_A kT.                                                (19.57)

Молярная теплоемкость кристаллической решетки при высоких температурах не зависит от температуры (закон Дюлонга)

C_V= 3R.                                              (19.58)