Элементы сверхпроводящей электроники. Динамика кристаллической решетки. Магнитные квантовые эффекты в полупроводниках, страница 13

На рис. 20.8 представлена зависимость  от  для трех образцов    GaAs / Al Ga As, содержащих двумерный вырожденный электронный газ. По графикам рис. 20.9 зависимости положения максимумов осцилляций  от номера осцилляции определялись периоды осцилляций 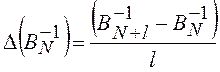. По формуле (20.23) вычислялась концентрация свободных электронов. Для      образца 1 концентрация    = (7,72 ± 0,05)·10¹¹ см^–2,  для образца 2       = (4,03 ± 0,07)·10¹¹ см^–2, для образца 3  = (8,45 ± 0,02)·10¹¹ см^–2. Значения концентраций электронов совпадают с погрешностью ~ 5 % с значениями , полученными холловскими измерениями.

Из (20.18), (20.19) и (20.23) с учетом полученных значений концентраций следует, что  > . В этом случае заполняется электронами нулевая подзона, образованная квантоворазмерным уровнем .

В случае заполнения электронами двух подзон, образованных квантоворазмерными уровнями  и , наблюдается суперпозиция осцилляций Шубникова - де Гааза с разными периодами . Это дает возможность рассчитать концентрации электронов в подзонах по формуле (20.23). При этом возникает необходимость исследовать гармонический состав осцилляций Шубникова - де Гааза. В случае заполнения электронами двух подзон, образованных квантоворазмерными уровнями  и , осцилляции Шубникова - де Гааза содержат кроме двух частот (двух периодов ) комбинации этих частот. Для нахождения частот (периодов ) необходимо проводить фурье - анализ осцилляций Шубникова - де Гааза. Периоды  определяются по положению пиков кривой спектральной плотности. Двумерные концентрации электронов в подзонах размерного квантования можно определять из максимумов фурье - спектров.

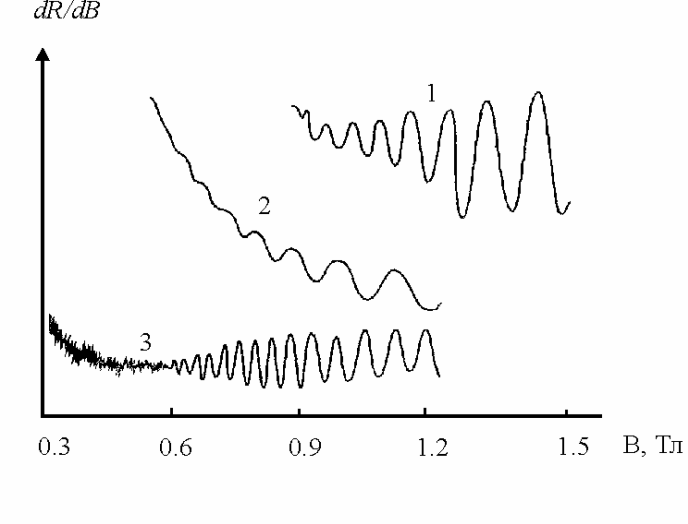
Рис. 20.8. Магнитополевая зависимость производной коэффициента отражения dR/dB для трех образцов CaAs/AlGaAs.

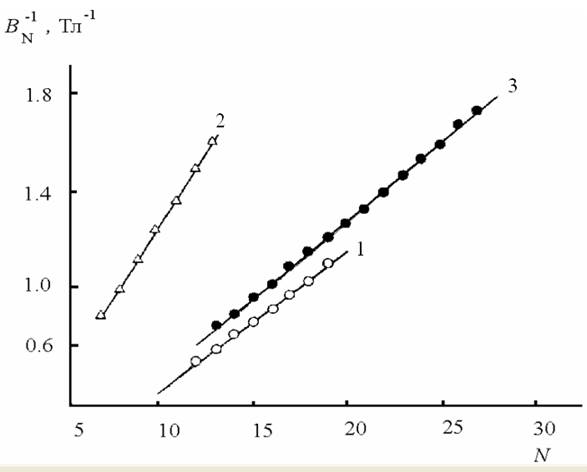
Рис. 20.9. Зависимость положения максимумов осцилляций  от номера осцилляции N для образцов 1,2,3 CaAs/AlGaAs.

Холловское сопротивление . Это соотношение справедливо для объемных и двумерных структур, содержащих вырожденный электронный газ. С учетом соотношений (20.21) выражение для определения холловского сопротивления

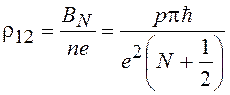                       ,                                       (20.24)

где = 1 или 2 в зависимости от величины магнитного поля. В области магнитных полей до 5 Тл для GaAs/AlGaAs влияние спина электрона на положения максимумов осцилляций Шубникова - де Гааза незначительно. В случае сильных магнитных полей при малых  проявляется расщепление максимумов, обусловленное влиянием спиновых подуровней на значения . При этом  2 и 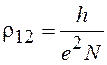 (целочисленный квантовый эффект Холла). При больших значениях  и соответственно меньших значениях магнитного поля  монотонно изменяется и квантовый эффект Холла не проявляется.

Периоды осцилляций Шубникова - де Гааза в СВЧ – методе совпадают с периодами осцилляций Шубникова - де Гааза в магнитосопротивлении. При выполнении осцилляционного условия максимумы поперечного магнитосопротивления ρ₁₁ совпадают с максимумами диссипативной диагональной компоненты тензора удельной проводимости σ₁₁. При σ₁₁<< σ₁₂

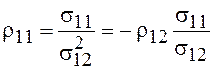                     .                                          (20.25)

Когда уровни Ландау перемещаются при изменении магнитного поля В диссипативная σ₁₁ и недиссипативная σ₁₂ компоненты тензора электропроводности демонстрируют различное поведение, а именно, σ₁₁ осциллирует, а σ₁₂ изменяется скачкообразно. Скачкообразный характер изменения σ₁₂ проявляется при выполнении осцилляционного условия (E_F = E_N). Изменения ρ₁₂ и σ₁₂ соответствуют максимумам σ₁₁. Когда осцилляционное условие не выполняется и уровень Ферми E_F находится в энергетической щели, образованной уровнями Ландау E_N, то в зависимости ρ₁₁ и σ₁₁ образуются глубокие провалы, размеры которых характеризуют качество 2D – слоя. В бесконечном образце с исключительно гладкими поверхностями перехода при Т = 0  σ₁₁ = 0,  ρ₁₁ = 0 и ток должен протекать без диссипаций. При T > 0 проводимость σ₁₁ отлична от нуля, но экспоненциально мала, за исключением тех моментов, когда уровень Ландау проходит через уровень Ферми. В реальных образцах существенно влияние примесей и неоднородностей 2D – слоя. В результате рассеяния на примесях, неоднородностях, а также теплового рассеяния носителей происходит уширение уровней Ландау и максимумы ρ₁₁ не являются острыми, а провалы ρ₁₁ не глубокими.