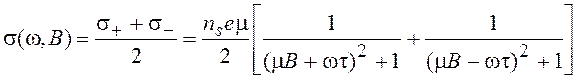Элементы сверхпроводящей электроники. Динамика кристаллической решетки. Магнитные квантовые эффекты в полупроводниках, страница 15

,               (20.28)

где и – компоненты эффективной проводимости, возбуждаемые волнами правой и левой круговой поляризации соответственно. При в области циклотронного резонанса и поглощение СВЧ мощности, в основном обусловлено проводимостью . Увеличение проводимости , обусловленное возрастанием поглощенной носителями СВЧ-мощности, вызывает уменьшение коэффициента отражения R. Изменение R можно представить линейной зависимостью от

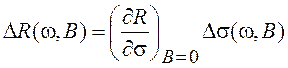.                               (20.29)

Производные ¶R/¶sи ¶R/¶Bимеют противоположные знаки.

Производные ¶R/¶Bи ¶s/¶Bв области циклотронного резонанса достигают экстремальных значений при

.                                   (20.30)

Вторые производные ¶²R/¶B²и ¶²s/¶В² максимальны при

.                                   (20.31)

Производная ¶R/¶B=0 при циклотронном резонансе

,                                   (20.32)

где – циклотронная частота,

m*- эффективная масса носителей заряда.

Подвижность и время релаксации импульса носителей определяются выражениями

,                                   (20.33)

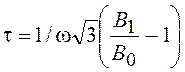.                                   (20.34)

При известной эффективной массе носителей

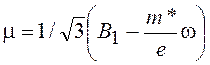,                                   (20.35)

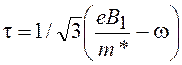.                                   (20.36)

Из (20.31) и (20.32)

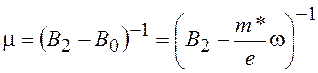.                             (20.37)

Из (20.33) и (20.37)

.                             (20.38)

В области магнитоплазменного резонанса [29] можно представить в приближенном виде, произведя в (20.28) замену wt на a

.                                           (20.39)

Из условия магнитоплазменного резонанса () определяется плаз-менная частота

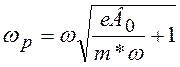.                                             (20.40)

При  подвижность  и время релаксации t определяются из соотношения

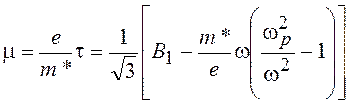                             (20.41)

Следует отметить, что из (20.40) и (20.41) получаем выражение (20.33).

Для оценки допустимости принятых приближений на рис.20.10 приведены магнитополевые зависимости высокочастотной проводимости и ее производных, рассчитанные в относительных единицах по следующим формулам:

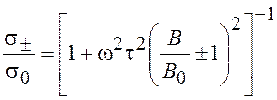,                              (20.42)

,                         (20.43)

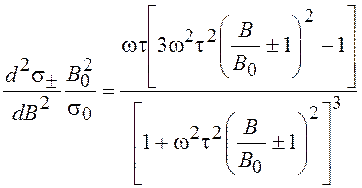.                       (20.44)

Из анализа кривых рис.20.10 следует, что при wt=1 выполняется приближение . Учет производных от уменьшает значения магнитного поля B₁ и B₂ на 1% и практически не изменяет их разность B₂^_B₁. Подвижность электронов, определенная по формулам (20.33) и (20.38) составляет m=11м²/Вс. На рис.20.11 представлены экспериментальные зависимости производных коэффициента отражения ¶R/¶В и ¶²R/¶В² от магнитного поля, полученные в [28,29] для 2D слоя GaAs гетероструктуры GaAs/Al_xGa_1xAs с концентрацией электронов n_s=2.5^.10¹¹  см^-2 при Т=80К и n=36,4 ГГц.

Из анализа кривых рис.20.11 получены значения магнитного поля B₀=0.091Тл, B₁=0.21Тл и B₂=0.30Тл. Подвижности электронов, определенные по (20.33) и (20.38) соответственно, составляют m₁=4.8м²/Вс и m₂=4.7м²/Вс. Полученные результаты согласуются с паспортным значением m_п=4.8м²/Вс для структуры, из которой был изготовлен образец. Время релаксации импульса электронов, определенное по формулам (20.34) и (20.38), составило t =1.9^.10^-12с. На основе полученных результатов wt составляет 0,437. Значения магнитного поля B₁ и B₂, полученные по формулам (20.43) и (20.44) без учета производных от , составили B₁=0.211Тл и B₂=0.299Тл. Учет влияния производных от приводит к уменьшению B₁ и B₂ на 10%. При этом разность B₂^_B₁ уменьшается лишь на 1%. Подвижность электронов, вычисленная по формуле (20.38) без учета влияния, составила m=4.8м²/Вс, а с учетом производных от  - m=4.85м²/Вс.

Для определения m и tрассмотренным методом не требуется измерять абсолютные значения коэффициента отражения и размеры исследуемого слоя образца. Этим методом можно определять m и tкак в двумерных системах, так и в объемных полупроводниках и тонких эпитаксиальных пленках