Элементы сверхпроводящей электроники. Динамика кристаллической решетки. Магнитные квантовые эффекты в полупроводниках, страница 6

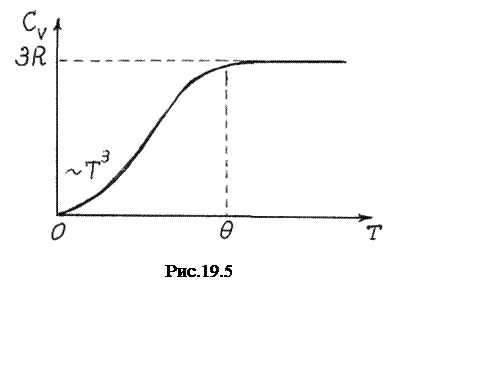
Квантовая теория теплоемкости твердых тел  удовлетворительнo согласуется с экспериментом и при   включает в себя классическую теорию. Теплоемкость кристаллов практически полностью объясняется теплоемкостью фононного газа. В заключение следует отметить, что фононы взаимодействуют друг с другом, с фотонами, с электронами и дырками, а также с дефектами кристаллической решетки (с вакансиями, дислокациями, поверхностью кристалла, атомами примеси). Рассеяние свободных электронов и дырок на фононах позволяет объяснить зависимость электросопротивления полу-проводников от температуры.

Электроны, излучая и поглощая фононы, при-тягиваются друг к другу. Это приводит к сверхпроводимости многих металлов, сплавов и полупроводников при низкой температуре.

Вопросы и задачи

1. В чем состоит принципиальное отличие координаты тела, колеблющегося на пружине, от нормальной координаты линейной атомной цепочки?

2. Показать, что энергия квантового гармонического осциллятора квантована и равна Е_n = (n + 1/2).

3. Каковы отличительные характеристики фононов и фотонов?

4. Показать, что энергия кристаллической решетки при высоких температурах пропорциональна T, а при низких температурах ~T⁴.

Г Л А В А  20

МАГНИТНЫЕ КВАНТОВЫЕ ЭФФЕКТЫ В ПОЛУПРОВОДНИКАХ

§ 20.1. Эффект Шубникова – де Гааза в объемных полупроводниках

В основе многих квантовых осцилляционных и резонансных эффектов лежит квантование энергии электронов в твердом теле под действием магнитного поля. Квантовомеханическая задача о движении заряженной частицы в однородном магнитном поле впервые была решена Ландау [18,19,20]. Им было показано, что для электронов с квадратичным законом дисперсии в магнитном поле  энергия электрона E зависит от квантовых чисел N и σ и проекции импульса электрона ћK_Z на направление магнитного поля

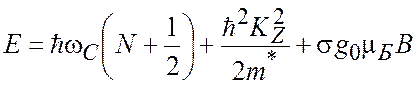             ,                  (20.1)

где 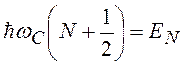 - энергия уровня Ландау, N = 0,1,2,3,··· – номер уровня Ландау,  – спиновое квантовое число, g₀ = 2 – фактор спинового расщепления энергии свободного электрона,  - магнетон Бора,  - циклотронная частота, m_n^* - эффективная масса электрона. Схема энергетических уровней электронов и графическая зависимость энергии от волнового вектора представлены на рис. 20.1.

Плотность состояний в магнитном поле с учетом квантования движения электронов проводимости существенно отличается от плотности состояний в отсутствие магнитного поля. В простейшем случае без учета спинового расщепления плотность состояний

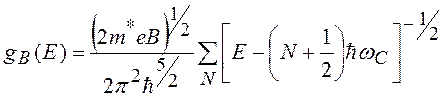                                      (20.2)

Зависимость плотности состояний от энергии представлена рис. 20.2.

Когда энергия электрона проводимости Е совпадает с энергией уровня Ландау, плотность состояний  Значение  практически становится конечным в результате теплового уширения энергетических уровней. Изменение плотности состояний можно вызвать, изменяя величину магнитного поля , либо изменяя энергию электрона . Изменение  может быть обусловлено изменением разности потенциалов, концентрации, температуры, давления и других физических величин. При изменении E и B плотность состояний испытывает осцилляции. Это приводит к осцилляциям кинетических, оптических и термодинамических параметров полупроводников и металлов, которые в настоящее время объединены общим названием квантовых осцилляционных эффектов.

При этом многие классические представления о механизме проводимости теряют смысл, носители заряда сильно взаимодействуют с кристаллической решеткой и природа проводимости носит чисто квантовый характер. Теория в этом направлении интенсивно развивалась с начала шестидесятых годов и возникла квантовая теория явлений переноса в квантующих магнитных полях.

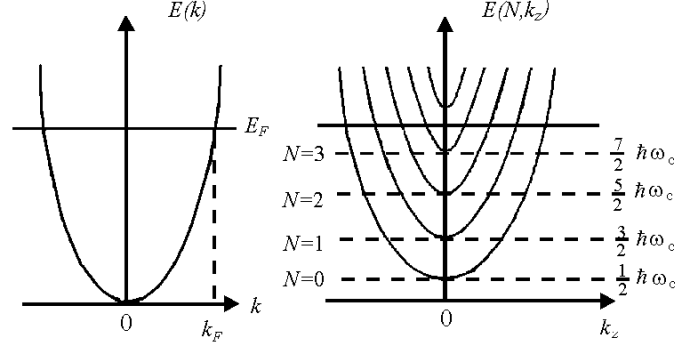
а                                                      б

Рис.20.1. Зависимость энергии от волнового вектора: а) в отсутствие магнитного поля и б) при наличии магнитного поля появляются дискретные уровни Ландау и одномерные зоны.