Локальность измерений определяется фокусировкой зондирующего излучения и в данном исследовании составляла ~ 140 мкм. Сканирование лазерного луча вдоль поверхности образца позволяло разрешать неоднородности концентрации, создаваемые неоднородным распределением легирующих примесей в областях ~ 100 мкм с погрешностью ~ 0,5%.
Значения концентраций свободных носителей для восьми образцов n-InSb, определенные разработанным нами методом, совпадают с точностью не хуже 5,0% со значениями, полученными из холловских измерений.
§ 20.3. Определение параметров полупроводников по магнитофононным осцилляциям
Магнитофононные осцилляции магнитосопротивления происходят в результате резонансного неупругого рассеяния носителей на полярных оптических фононах благодаря малой дисперсии оптической ветви вблизи центра зоны Бриллюэна и резкому возрастанию плотности состояний вблизи уровня Ландау. При совпадении энергии оптического фонона с энергетическим интервалом между любыми уровнями Ландау происходит резкое увеличение вероятности рассеяния из-за резонансного возрастания плотности начального и конечного состояний для процессов поглощения и испускания оптических фононов электронами.
В отличие от осцилляции Шубникова – де Гааза магнитофононные осцилляции могут проявляться при любой степени вырождения электронного газа полупроводника только при неупругом рассеянии носителей заряда и по сравнению с гелиевой высокой температуре. С увеличением температуры вероятность испускания оптических фононов растет. При энергии оптического фонона ħω0 больше k0T амплитуда магнитофононных осцилляций экспоненциально растет с повышением температуры. Однако температура должна быть лишь относительно высокой, когда определенное количество оптических фононов возбуждено. С другой стороны, температура должна быть ограничена сверху условиями ħωС > k0T и ωCτ >1.
В полупроводниках с вырожденным электронным газом и непараболичной зоной проводимости магнитофононные осцилляции должны проявляться при EF >> ħω0 > ħωC и выполнении осцилляционного условия Kz = 0.
На рис.20.5 приведены магнитофононные осцилляции магнито-сопротивления образца n-InSb (n = 1,3.1014см-3, mn = 6,4.105 см2/Вc, Т = 77K).
Период осцилляции по
обратному магнитному полю не зависит от магнитного поля и составляет 
= 0,29 Тл-1.
Частота продольных оптических фононов в InSb известна из экспериментов по комбинационному рассеянию света νо = 5,9·1012 Гц. Учет непараболичности зоны проводимости InSb приводит к неэквидистантности уровней Ландау. В этом случае осцилляции не строго периодичны в зависимости B-1.
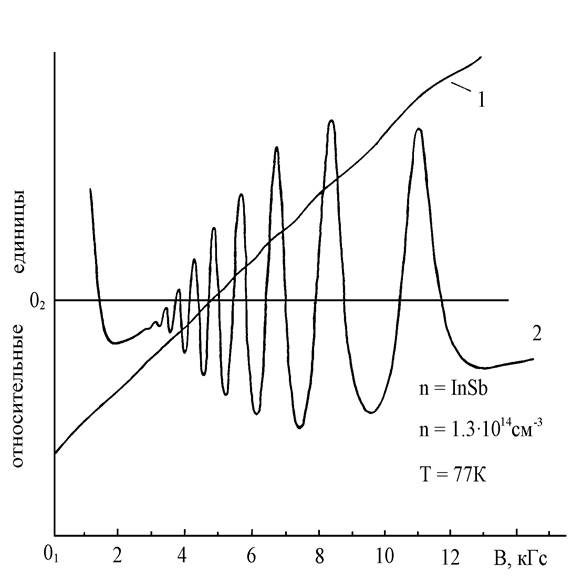
Рис. 20.5. Магнитофононные осцилляции в n - InSb (n = 1,3×1014 см-3, mn = 6,4×105 см2/Вс, Т=77 K). 1 - поперечное магнитосопротивление r. 2 - вторая производная магнитосопротивления (-¶ 2r/¶B2).
Выражение для определения 
с учетом непараболичности зоны
проводимости имеет вид:
(20.6)
Для InSb ∆0 = 0,9 эВ, Eg= 0.236 эВ, ħω0 = 24 мэВ.
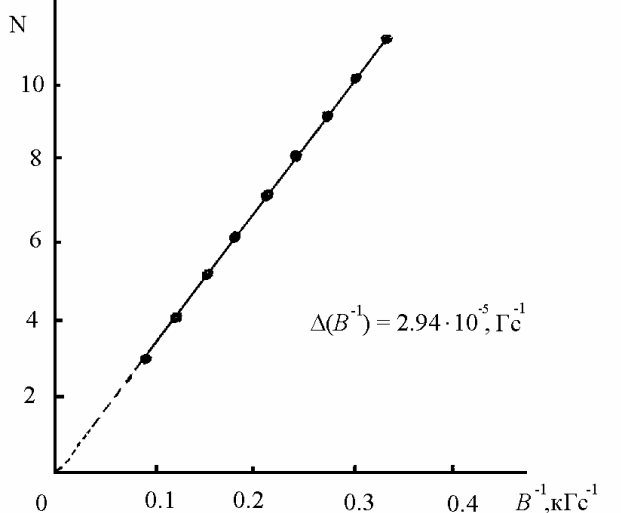
Рис. 20.6. Зависимость положения максимумов магнитофононных осцилляций от обратного магнитного поля.
Поправка к значению 
на непараболичность зоны
проводимости InSb составляет 17%. Из графика
зависимости B-1 от 
рис.20.6 положение первого максимума
B1 =3.4Тл. При ω0 = 2πν0 = 3,7·1013с-1 и B1 = 3,4 Тл получаем значение эффективной массы электронов
вблизи дна зоны проводимости /m0 = 0,013, согласующееся с известными
экспериментальными данными.
§ 20.4. СВЧ осцилляции Шубникова - де Гааза в двумерных гетероструктурах GaAs/Alx Ga1-x As
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.