Методика анализа традиционного процесса решения проектно-конструкторских задач, страница 8

·  его интерпретацию.

С математической точки зрения мы имеем здесь частный вид абстрактной алгебры (булева алгебра).

Но сам по себе аппарат булевой алгебры не является логическим.

Он может иметь и иные интерпретации, например, в терминах теории релейно-контактной схемы:

И (&)

Y	X1	X2
0	0	0
0	0	1
0	1	0
1	1	1

следовательно логическая схема

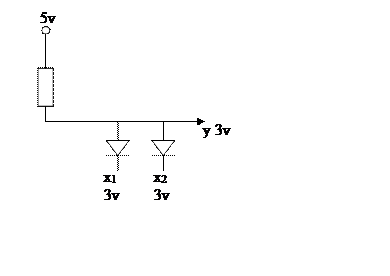
контактная схема

или (v)

Основным здесь является тот факт, что значение истинности любого сложного высказывания, построенного из простых высказываний и логических связок есть функция истинности простых  высказываний.

Аргументы и функции принимают значения истина и  ложь (здесь заключаются основы композиционного метода предикатов). Таким образом применение аппарата булевой алгебры предполагает предварительный этап эмпирического анализа в ходе которого названные логические связки обнаруживаются в языке, а их свойства получают явные описания. Следует подчеркнуть этот момент:

Формализация каких-то смысловых структур в языке, построение или использование математических моделей предполагает существующим новых выделения в материале естественного языка соответствующих смысловых структур в сложившуюся и социально закрепленную языковую интуицию, которая позволяет вычленить, распознать определенные единицы содержания не зависимо от способа их выражения, отождествлять разные конструкции естественного языка как равные по смыслу.

История развития логики свидетельствует, что для выделения в языке простых конъюнкций и импликаций потребуется исторически длительный, отнюдь не прямой, путь. Относительно импликации споры продолжаются до сих пор.

Парадоксы материальной импликации

1.  Если 2∙2=4, то NewYork – большой город

2.  Если 2∙2=5, то NewYork – большой город

3.  Если 2∙2=4, то NewYork – маленький город.

4.  Если 2∙2=5, то NewYork – маленький город.

В повседневной речи эти высказывания вряд ли будут рассматриваться как имеющие смысл и еще в меньшей степени как истинные. С точки зрения математической логики все они осмыслены, причем второе высказывание ложно, остальные истинны.

1.  Если 2∙2=4 (Истина), то NewYork – большой город (Истина).

2.  Если 2∙2=5 (Ложь), то NewYork – большой город (Ложь).

3.  Если 2∙2=4 (Истина), то NewYork – маленький город (Истина).

4.  Если 2∙2=5 (Ложь), то NewYork – маленький город (Истина).

Формальный аппарат логики высказываний дает средства для решения двух основных задач:

1 задача:

Дано сложное высказывание F, построенное из простых высказываний х₁, х₂, … х_n и логических связок, а так же значений простых высказываний. Требуется определить значение истинности сложного высказывания F.

2 задача:

Даны 2 сложных высказывания F и G, построенные на основании простых высказываний х₁, х₂, … х_n и y₁, y₂, … y_m (не обязательно разных), а так же логических связок (и, или, не и т.д.). требуется определить – верно ли, что из F логически следует G.

Вторая задача в некотором смысле сводится к первой, а именно: понятие логического следования уточняется с помощью понятия истинности.

Например, из F логически следует G  если только F→G – тождественно-истинное высказывание (является тавтологией логики высказываний).

Принятие именно такого определения предполагает, что имеется предшествующее какой бы то ни было формализации содержательное (интуитивное) понимание логического следования. Оно сводится к двум основным пунктам:

1.  из F логически следует G, если

·  во-первых, при истинности F не может быть ложным G. Иными словами F&~G (или F&G–  ) - не возможно;