Методика анализа традиционного процесса решения проектно-конструкторских задач, страница 7

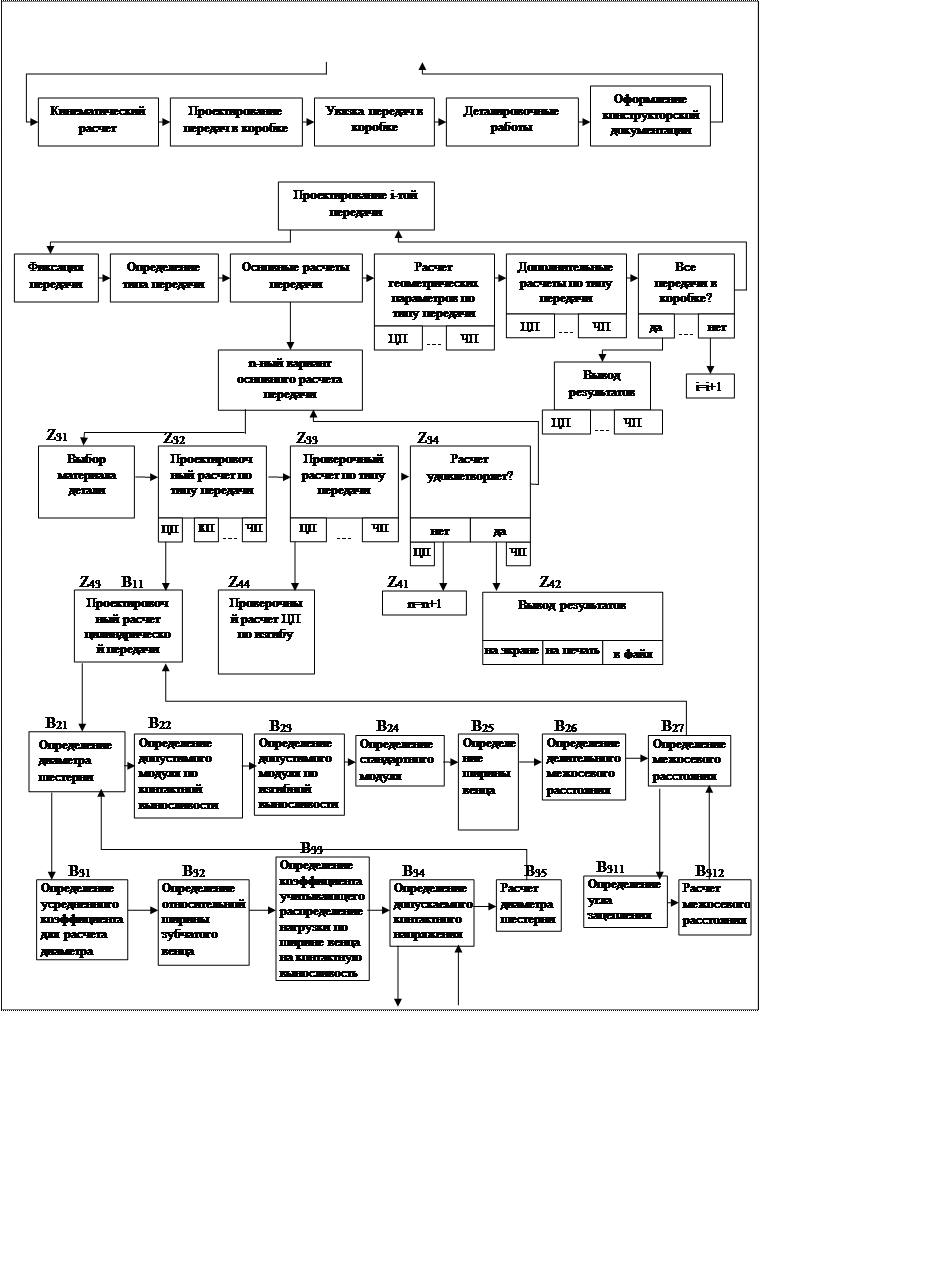
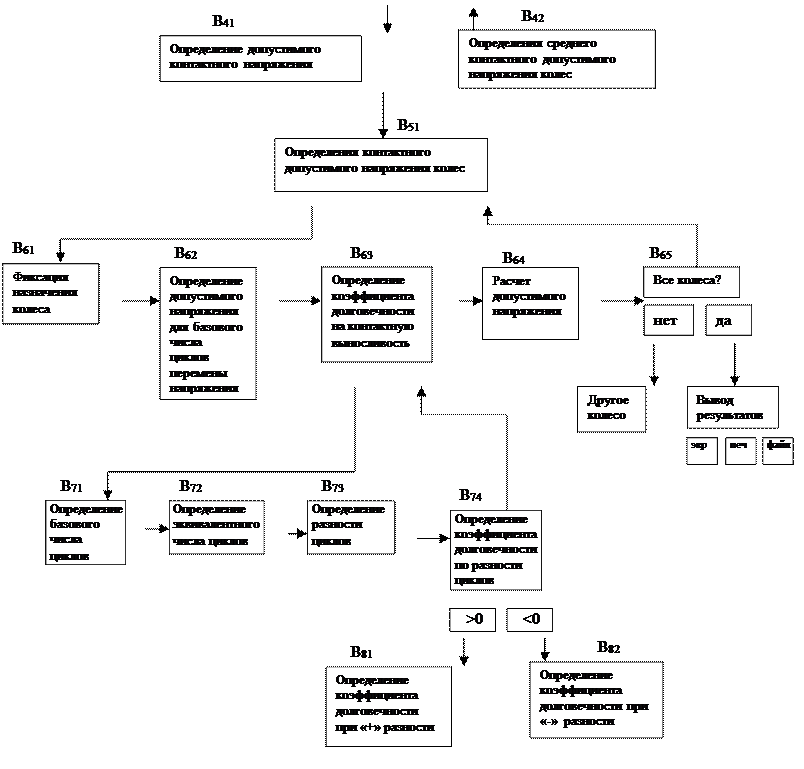
5.5.2  Пример описания модельного представления задачи (коробка передач)

Существуют определенные методики проектирования любого изделия.

Проектирование коробки передач

 

Форма А:

Код задачи: ОРП

Код ПД1	Код ПД2	Код ПД3	Вид компоновки
Z11	Z21	=	Цикл
Z21	Z31	Z32	Последовательность
…	…	…	…
Z34	¥41	Z42	Переключатель

Код задачи: ЦП₁

Код ПД1	Код ПД2	Код ПД3	Вид компоновки
в11	в21	в22	Последовательность
в11	в22	в23	Последовательность
…	…	…	…
в74	в81	в82	переключатель

Форма В: Описание предметных действий.

Код задачи: ОРП

Код ПД	Наименование предметного действия	Степень формализации	Статус
Z11	Основные расчеты передач	Аналитическая	П
Z21	Выбор материала	Алгоритмическая	КЭ
Z31	Выбор деталей передачи	Алгоритмическая	КЭ

5.6 Логика и язык науки

Развитие символической логики дало крупные результаты в исследованиях по основам математики, тогда как за пределами этой области – там, где речь идет об анализе языка эмпирической науки достижения логического анализа пока более чем скромные. Между тем, концептуальные основания, например, физика или гуманитарные науки ничуть не меньше нуждаются  в логической разработке, чем основания математики.

Программа создания универсального и полностью контролируемого логическим анализом языка науки осталась невыполненной.

Возникает вопрос о причинах такого положения. Временная ли эта неудача или принципиальная невозможность логических унификаций (предикатов) языка науки.

Тема эта актуальна, интерес к ней не утрачен. Об этом говорит факт появления все новых языков представления знаний. Поэтому полезно разобраться где лежат действительные проблемы формализации естественного языка и где их нет.

Истинность исследования

В дискуссиях сравнительно недавнего прошлого много говорилось об экстенсиональном характере построения классической математической логики и их несоответствии интенсиональному характеру связей в естественном языке. Экстенсиональность здесь видят в том, что классическая математическая логика рассматривает якобы суждения только с точки зрения их истинности, но не содержания. Рассматривают связь суждений по значениям истинности, но не рассматривают связь по смыслу.

Другой аргумент состоит в том, что ставится под сомнение универсальность математической логики. При этом стремятся доказать, что аппарат классической математической логики не применим для описания объектов того или другого вида:

·  применим в макромире, но не применим в микромире;

·  применим для описания простых объектов, но не применим для описания сложных.

Существует точка зрения, что данные утверждения основаны на недоразумении.

Нет серьезных оснований говорить о неадекватности языка классической математической логики задаче формализации профессиональных знаний. Для более конкретного обсуждения обратимся к логике высказываний, которая составляет фундамент других логических построений, представляет собой простую и хорошо обозримую удобную модель.

Классическая логика высказываний может рассматриваться как алгебра и как  логика.

Здесь необходимо различать:

·  собственно математический аппарат;