Исследование возможности упрочнения стекла лазерным излучением, страница 17

Гистограмма - это кусочно-постоянная функция

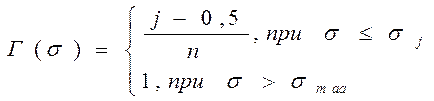                       (2,7)

Для аппроксимации этой построенной по экспериментальным данным функции чаще всего применяется функция распределения Гаусса - нормальный закон распределения:

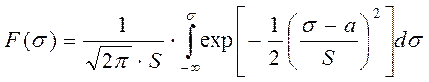,                      (2.8)

где S и a - параметры распределения.

Причем, a - среднее значение случайной величины, S - стандартное отклонение.

Нормальный закон распределения применим при небольшом разбросе экспериментальных данных. При V=0,2 он дает хорошее приближение среднего значения случайной величины. Недостатком этого закона распределения является ненулевая вероятность существенная отрицательных значений случайной величины, что при обработке результатов испытаний на прочность не имеет смысла.

В теории хрупкой прочности часто пользуются функцией распределения Вейбула, которая в интегральной форме имеет вид:

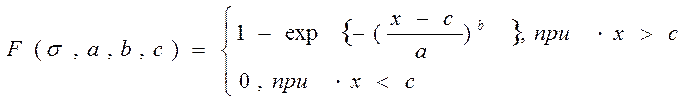, (2.9)

где  a, b, c- параметры функции распределения; а - значение прочности, при котором F(σ)=0,63;

b - параметр гомогенности (однородности);

с - наименьшее значение прочности.

Распределение Вейбула предлагает нулевую вероятность существования отрицательных значений прочности и хорошо аппроксимирует экспериментальные данные в области нижних значений, которые наиболее важны в хрупкой прочности. Параметр гомогенности b характеризует однородность материала. Чем больше значение b, тем однороднее материал.

При аппроксимации экспериментальных данных функциями (2.8) или (2.9) следует проверить соответствие выборок этим законом распределения. Проверку можно осуществлять графически, используя так называемую вероятностную бумагу, на которой за счет подбора масштаба функции (2.8) или (2.9) сводятся к линейным.

Если экспериментальные точки хорошо аппроксимируются прямой линией, на соответствующей, предполагаемому закону распределения вероятностной бумаге, то можно сделать вывод о соответствии экспериментальных данных этому закону распределения.

Более точно проверку соответствия закону (2.8) или (2.9) можно проводить по критерию согласия Пирсона. Этот критерий требует большого количества испытаний (n>100) и предварительной оценки параметров распределения. При применении критерия Пирсона область изменения случайной величины разбивается на интервалы. Число интервалов l зависит от объема выборки. При n = 100 обычно принимают l= 10-15. Интервалы, содержащие менее пяти наблюдений случайной величины объединяют с соседними. После этого, вычисляется величина:

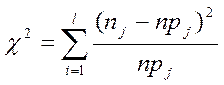,                                      (2.10)

где  p_j - вероятность попадания в j-й интервал, вычисляемая в соответствии с гипотетическим законом распределения (2.8) и (2.9).

Если выполняется неравенство χ²≤ χ_α²_, где χ_α² находится по таблице (6.3) значения χ² для числа степеней свободы k= l₁-m-1 (здесь l₁ - число интервалов после объединения, m - число оцениваемых параметров), то гипотезу о соответствии выборки данному закону распределения не отвергают.

3.1.5 Условия проведения испытаний

Образец для испытаний должен иметь форму квадратной пластины показанной на рисунке 2.19. Размер квадратной пластины, диаметры опоры и нагружающего пуансона в зависимости от толщины образца приведены в таблице 2.3.

На поверхности образцов, подлежащих испытанию, не должно быть трещин, сколов или других дефектов, видимых без увеличительных приборов.

 

100 ±1,0                                                                 5 ±0,5

Рис. 2.19Образец для испытаний.

Таблица 2.3.Размерыобразцов.

Количество образцов, необходимое для определения с заданной точностью среднего значения прочности или нижних значений (квантилей нижних уровней) следует выбирать по таблице 2.2.