Методичні вказівки до лабораторних робіт з дисципліни «Основи метрології, стандартизації та управління якістю», страница 7

Для    знаходження    випадкової   складової    похибки   Δ_в у кожному полі потрібно визначити середнє квадратичне відхилення σ_j на кожному j-му полі нормалізованої шкали (j = 1…12):

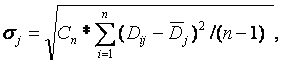
де  – поправочний коефіцієнт, що дорівнює 0,87. Він враховує об'єм вибірки, тобто відмінність отриманого значення середнього квадратичного відхилення від середнього квадратичного відхилення генеральної сукупності.

Випадкова складова Δ_вj похибки у кожному полі визначається за 3σ-границями:

                                                 Δ_вj =  ± 3 σ_j.                                            (1.7)

Систематична складова похибки Δ_сj для кожного (j-го) поля розраховується за дещо зміненим рівнянням (1.4):

                                         _{, дійсне}                                                        (1.8)

Дані розрахунків заносять у табл. 1.2.

          Таблиця 1.2 – Значення оптичної щільності та результати  розрахунків для нормалізованої шкали