Методичні вказівки до лабораторних робіт з дисципліни «Основи метрології, стандартизації та управління якістю», страница 17

Так, для нашого прикладу з табл. Б.1  для рівня значущості α = 0,05 при f₁ = f₂ = 4 визначаємо табличне значення   . Оскільки F = 1,19 <  (розраховане значення F-критерію менше табличного значення), гіпотеза про рівність дисперсій двох нормально розподілених сукупностей приймається. Це свідчить про  незмінність точності ТП виготовлення фотоформ у часі.

По-друге, треба перевірити статистичну гіпотезу про рівність двох середніх нормально розподілених генеральних сукупностей:

Н₀ : m₁ = m₂                                                                             (2.7)

за критерієм Стьюдента (t-критерієм). При цьому оцінюється розходження двох вибіркових середніх. Якщо вибірки беруться з нормальних сукупностей, то величина

(2.8)

підпорядковується розподілу Стьюдента. Для розглянутого прикладу при числі степенів свободи f =– 2  =  5 + 5 – 2 (п₁ , п₃ – розмір першої та третьої вибірки відповідно):

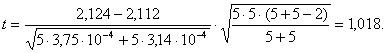
Якщо розраховане значення  t < t_табл, то гіпотеза приймається, у протилежному – не приймається.

З довідкової табл. Б. 2 для  f = 5 + 5 – 2 = 8   і   α = 0,05  вибрали табличне значення t_а,f = 2,31. У таблиці  Б.2  рівень значущості α задається у процентах, тому для наведеного прикладу вибираємо α = 5.

Оскільки   t = 1,018 < t_α,f = 2,31, то гіпотеза (2.7) приймається, що свідчить про незмінність центру налагодження за період між першою та третьою вибірками.

Для обчислення, S², t можна скористатися стандартними програмами, наприклад, Microsoft Excel.