1. Система уравнений (8.2) (разд. 8) записывается в каноническом виде (9.6): производные записаны через символ d/dt, искомые функции – в виде явных функций времени, нижние индексы переведены в имена функций, все члены сгруппированы влево, знак "равно" вставлен с панельки Boolean или сочетанием клавиш <Ctrl >+ <=>. Эта запись носит справочный и технологический характер.
Примечание. При наличии нижних индексов Mathcad выдает внешне правдоподобные, но не верные результаты в рассмотренных вычислениях.

(9.6)
P0 (0) = 1, P1(0) = P2(0) = P3(0) = 0. (9.7)
![]() (9.8)
(9.8)
2. Копируется левая часть первого уравнения системы (9.6), выделяется в любом месте копии переменная t, командой меню «Symbolics-Transform-Laplace» (или кнопкой <laplace> на панельке Symbolic) в конце копии вставляется оператор Лапласа laplace, < ® (этап 2), в его место ввода вставляется переменная t дифуравнения и клавишей <Enter> инициируется процесс преобразования: Mathcad выдаст L-изображение левой части в виде (9.9).
Это изображение копируется и упрощается вручную с учетом начальных условий типа (9.7) и с заменой длинных имен изображений вероятностей, данных Mathcad, на укороченные (например, laplace(Р0(t),t,s) = Р0), как показано в (9.10).
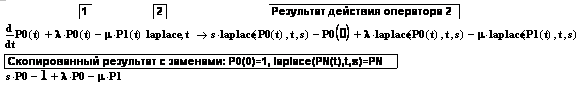
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.