Функциональное решение линейных дифференциальных уравнений и их систем (задача Коши) методом прямого и обратного преобразования Лапласа, страница 2

9.1.1. Определение L-изображения неизвестной функции х(t)                                            дифференциального уравнения

Рассмотрим функциональное решение дифуравнения (9.1) с начальными условиями и функцией времени 1,4×sin(3×t) в задающем воздействии:          

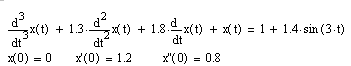                                                                                                                                                                                        (9.1)

Численное решение его с помощью функции rkfixed и график х(t) имеет вид: рис. 9.1. Для того, чтобы найти L-изображение х(t) (т.е. Х(s)), необходимо перевести дифуравнение (9.1) в пространство L-изображений. Возможны три способа такого перевода: целиком уравнение (9.1) через кнопку laplace на панельке Symbolic (рис. 9.2, А), по отдельным слагаемым с производными (или по группам с такими слагаемыми) и группе слагаемых без производных через кнопку laplace на панельке Symbolic с последующим суммированием результатов (рис. 9.2, Б), путем ручного ввода в РДМ изображений отдельных слагаемых (с производными и без них) с использованием формулы (9.5) и таблицы L-преобразований (табл. 9.1) –  рис. 9.2, В.

 

Рис. 9.1. А - решение дифуравнения (9.1);Б - график                     

решения х(t); В – измерение максимального выброса

Правила 1 получения L-изображения X(s) неизвестной функции x(t)                                                при преобразовании линейного дифуравнения целиком (рис. 9.2, А)

1.  Дифуравнение представляется в виде уравнения с правой частью, равной нулю, т.е. правая часть дифуравнения переносится влево с обратным знаком.

2.  Для решения дифуравнения с использованием преобразований Лапласа следует открыть новый рабочий документ (РДМ), т.к. при наличии в РДМ некоторых вычислений Mathcad может отказать в выполнении L-преобразования. Этапы вычисления L-изображения X(s) на рис. 9.2, А пронумерованы.