Математика \ Математическое моделирование

Функциональное решение линейных дифференциальных уравнений и их систем (задача Коши) методом прямого и обратного преобразования Лапласа, страница 11

                                                                                                                                                                                       (9.14)

такая точка при t = 25 час (аналогичная точка показана на графике численного решения системы (8.2) –  рис. 8.2). Как следует из данных этих точек относительная разность raznР0 между численным и функциональным решениями равна:

                   raznР0 = (0,99086 – 0,99074)/0,99074 = 0,00012, т.е. 0,012%.                                                              (9.15)

                                                                          

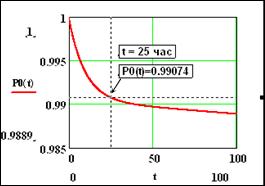
Рис. 9.4. График Р0(t) из (9.14) и измерительная точка при t=25 час                                                                                  для проверки правильности определения Р0(t) как решения системы (9.6)

9.3.  Упражнения

Выборочные упражнения

№ п/п

Задание

Методика,

№ раздела

Источник данных

1   

Функциональное решение дифуравнения посредством прямого-обратного преобразований Лапласа в Mathcad, построение графика решения, аналогичного рис. 8.3, вычисление измерительной точки графика и вычисление разности в измерительных точках численного решения из графика типа рис. 8.1 и функционального решения из графика типа рис. 8.3

9.1

Разд. 15.8.1, табл.15.8.1, тот же вариант, что применялся в разд. 8

2   

Функциональное решение системы диф­уравнений надежности САУ  посредством прямого-обратного преобразований Лапласа в Mathcad, построение графика решения Р0(t) или всех вероятностей САУ, аналогичного рис. 9.4.  Вычисление измерительной точки (точек) графика и вычисление разности в измерительных точках численного решения из графика типа рис. 8.2 и функционального решения из графика типа рис. 9.4  на графике для Р0(t)) или для всех вероятностей САУ

9.2

Разд. 15.8.2, табл.15.8.3, тот же вариант, что применялся в разд.8
Скачать файл