Функциональное решение линейных дифференциальных уравнений и их систем (задача Коши) методом прямого и обратного преобразования Лапласа, страница 5

 

                                                                                                                                                                                   +   

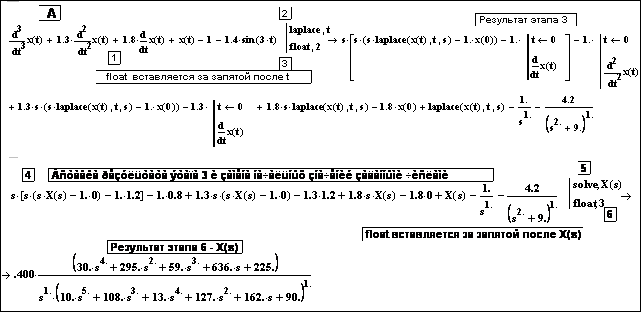
Рис. 9.2. Способы получения L-изображения X(s) искомой функции x(t) дифуравнения (9.1).                                   А – через L-преобразование целого уравнения (9.1); Б – через L-преобразование отдельных слагаемых и их групп уравнения (9.1) с последующим суммированием результатов; В –  посредством ручного ввода в РДМ изображений отдельных слагаемых с использованием формулы (9.5) и таблицы L-преобразований (табл. 9.1). Начальные значения х(0), х¢(0) и х¢¢(0) берутся из формулы (9.1). X(s) = laplace(x(t),t,s).                       На рис. 9.2, А преобразования laplace и float обозначены разными этапами, а на рис. Б и В – объединены в один этап

 

Продолжение рис. 9.2.

Правила 3 получения L-изображения X(s) неизвестной функции x(t)                                                путем ручного ввода в РДМ изображений отдельных слагаемых дифуравнения с использованием формулы (9.5) и таблицы L-преобразований (табл. 9.1) –  рис. 9.2, В

1.  Изображение к-й производной при ненулевых начальных условиях имеет вид: