Особенности выбора электродвигателя и системы электропривода для подъемно-транспортных машин. Построение диаграммы статических моментов для электродвигателя механизма подъем, страница 8

2.  Если электромагнитная постоянная времени силовой цепи соизмерима с периодом коммутации вентилей  управляемого преобразователя, то необходимо учитывать время запаздывания преобразователя , представляя его соответствующим звеном, или в первом приближении учесть в постоянной времени силовой цепи.

При кусочно-линейной аппроксимации нелинейных характеристик расчет динамических процессов ведется по этапам на каждом линейном участке с контролем за значением переменной, определяющей окончание участка. На каждом этапе составляются дифференциальные уравнения, определяются корни, находятся аналитические решения с учетом начальных и установившихся значений координат для данного отрезка аппроксимации. Рассмотрим на примере приведенной схемы при .

Решая (4.1) относительно скорости и момента учитывая, что 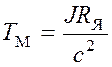 и что при отсутствии узла согласования, получим дифференциальные уравнения:

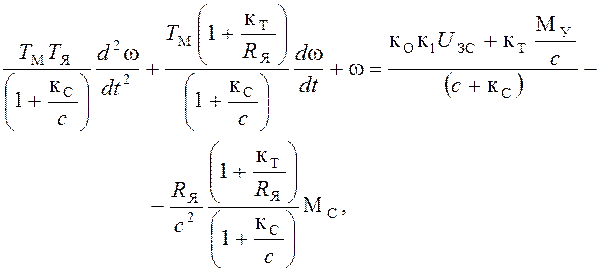   (4.6)

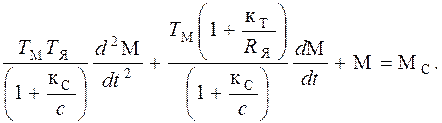            (4.7)

Правая часть уравнений (4.6) и (4.7) представляет установившиеся значения переменных. Корни характеристического уравнения системы:

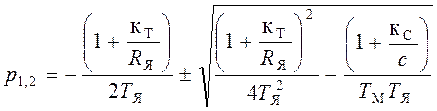.                (4.8)

Вид аналитических решений уравнений (4.6) и (4.7) определяется характером корней (4.8).

Процесс пуска происходит в несколько этапов, определяемых значениями тока якоря и момента.

I этап: . Протекает электромагнитный процесс, который описывается 1-м и 2-м уравнениями (4.1).При этом якорь неподвижен (ω=0), сигнал обратной связи по скорости отсутствует и ,  и . Дифференциальное уравнение:

.

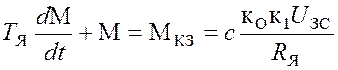Временная диаграмма представлена на рис.4.5.  

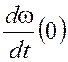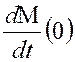II этап:   . Якорь ЭД начинает разворачиваться и выражения (4.6-4.8) записываются при условии: , а . Начальные условия ω(0)=0, , а начальные значения производных  и  определяются соответственно по 3, и 2и1 уравнениям (4.1). В частност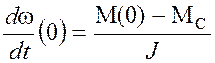и:  , и 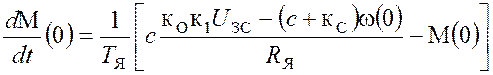. На рис. 4.6 приведены временные диаграммы процесса на данном этапе.

Конечные значения переменных на данном этапе .

III этап:  . Включена обратная связь по току, (4.6-4.8) записываются при условии:  и . Начальные значения переменных ω(0)=, , а начальные значения производных определяются аналогично, как и для предыдущего этапа, но с учетом действия обратной связи по току. Временные диаграммы скорости и момента показаны на рис. 4.7.

Окончание этапа в момент времени  при достижении моментом значения , а скорость

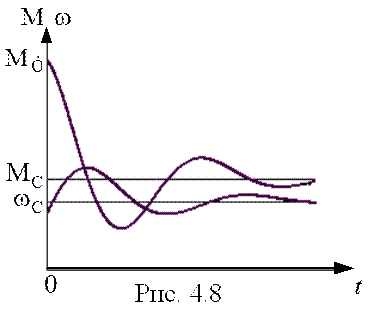
IV этап:   Обратная связь по току отключена и . Начальные условия для данного этапа . Значения производных определяются, как и в предыдущих случаях. Диаграммы для IV этапа на рис. 4.8.

Окончательно, полностью зависимости  и  при пуске на рис.4.9.

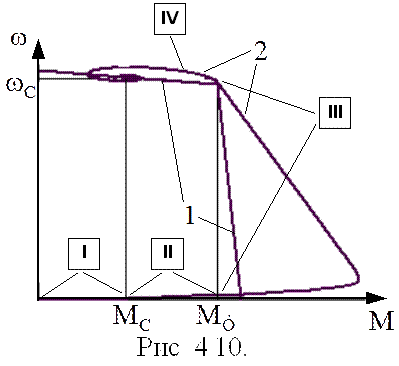
На рис 4.10. представлены механические характеристики системы, где: 1 – статическая и 2 – динамическая для процесса пуска (фазовая траектория) с указанием участков (I-IV):

4.2.1. Пример. Переходный процесс в системе с переменной структурой.

Переходный процесс пуска на холостом ходу до скорости входа резца в металл ЭП стола продольно-строгательного станка.

Используем данные предыдущего примера:R_Я=1.21 Ом, с=2.65, J=0.435 кгм², Т_Я=0.0175 с, Т_М=0.075 с, β_С=5.8, к_О=246, к_ОТ=1.6, к_Т=391, к_ОС=0.315, к_С=77.1, к₁=4.25, М_С=М_ХХ=9.5Нм, ω_С=13рад/с, ω₀=13.05рад/с, М_У=215 Нм, U_З=U_ЗСП=0.996 В.

I ЭТАП. Электромагнитный переходный процесс при неподвижном роторе, когда  Нм, к_Т=0 и к_С=0. Он описывается первыми уравнениями (4.1) и аналитическое решение

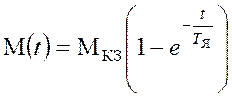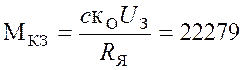, где Нм.

Данные расчетов сводятся в таблицу:

Графически аналитическое решение представлено на рис. 4.11.

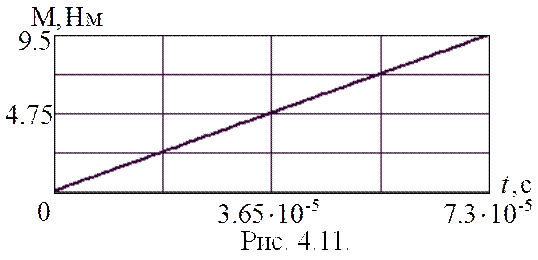
Конечные значения переменных: М_кон1=М_С и ω_кон1=0.

II ЭТАП. . Якорь ЭД начинает разворачиваться при отключенной обратной связи по току: к_С≠ 0, к_Т=0. Начальные значения переменных: ω(0)=ω_кон1=0, М(0)=М_кон1=М_С, 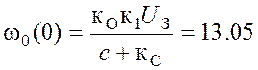 рад/с. Начальные значения производных: в соответствии с 3-м уравнением (4.1) 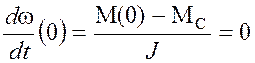 и с 1-м и 2-м уравнениями