Методические указания для выполнения курсового проекта по дисциплине «Металлорежущие станки», страница 9

По  количеству  зубчатых  передач  все  три  варианта  эквивалентны  (требуют  по  7  пар  зубчатых  колес).  Варианты  1  и  2  требуют  для  своей  реализации  4-х  валовой  конструкции,  вариант  3 – 3-х  валовой.  Поэтому  3-й  вариант  по  количеству  валов  был  бы  не  полным,  так  как  не  рассмотрена  возможность  применения  многоскоростного  электродвигателя.  Из  представленных  вариантов  только  вариант  2  позволяет  применить  2-х  скоростной  электродвигатель  (при  этом  группа  из  3-х  передач  должна  быть  основной,  электродвигатель – 1-й  переборной,  т.к.  1,26³ = 2).  

Механическая  часть  привода  в  этом  случае  будет  иметь  структуру  Z = 3 х 2,  требует  всего  5-ти  пар  зубчатых  колес  при  3-х  валовой  конструкции.  Следовательно,  в  данном  случае  наиболее  рациональной  является  кинематическая  структура  варианта  2.

Пример  2.  Спроектировать   привод  с  диапазоном  регулирования  D = 31,5  и  знаменателем  φ = 1,26

Для  получения  указанного  диапазона  необходимо  16  ступеней.  Возможные  варианты  кинематических  структур  следующие:

1)  Z = 2 х 2 х 2 х 2

2)  Z = 4 х 2 х 2

3)  Z = 2 х 4 х 2

4)  Z = 2 х 2 х 4

5)  Z = 4 х 4

Все  варианты  требуют  8-ми  пар  зубчатых  колес,  т.е.  по  этому  критерию  являются  эквивалентными.  Наибольшее  количество  валов  (5)  требует  1-й  вариант,  наименьшее  (3) – 5-й  вариант.  Следовательно,  по  этому  показателю  предпочтительным  является  вариант  5.  Однако  вариант  (5)  вообще  реализовать  нельзя,  т.к.  диапазон  регулирования  последней  переборной  более  8.  Вариант  4  можно  реализовать   только  при  условии,  что  группа  из  4-х  передач  не  будет  последней  переборной. Все  оставшиеся  варианты  (2,  3,  4)  не  позволяют  применить  многоскоростной  электродвигатель  и  являются  равнозначными.

Имея  в  своем  расположении  8  пар  зубчатых  колес  можно  применить  кинематическую  структуру  вида  Z = 3х3х2.  По  количеству  валов  и  зубчатых  колес  эта  структура  эквивалентна  ранее  рассмотренным,  но  позволяет  при  этом  в  1,58  раза  увеличить  диапазон  регулирования  и,  следовательно,  является  предпочтительной.  Кроме  того,  последний  вариант  позволяет  применить  3-х  скоростной  электродвигатель.  Механическая  часть  привода  в  этом  случае  будет  иметь  структуру  Z = 3х2,  требует  всего  5-ти  пар  зубчатых  колес  при  3-х  валовой  конструкции. 

Таким  образом,  проведенный  анализ  позволил  выявить  наиболее  рациональную  для  данного  случая  кинематическую  структуру.

При  анализе  возможных  вариантов  конструктивного  порядка  расположения  и  кинематического  порядка  распределения  предпочтение  отдается  тем  вариантам,  которые  обеспечивают  более  высокую  быстроходность  промежуточным  валам  привода.  Это  позволяет  уменьшить  крутящие  моменты  на  этих  валах,  что  в  свою  очередь  уменьшает  диаметры  валов  и  модули  зубчатых  передач,  снижает  материалоемкость  и  габариты  приводов.

Определение  чисел  зубьев  зубчатых  колес.      Числа  зубьев  должны  быть  выбраны  таким  образом,  чтобы  обеспечить  передаточные  отношения  всех  передач  согласно  графику  чисел  оборотов.  Погрешность  Δ  при  этом  не  должна  превышать  величины

Δ = ±10 (φ – 1), %                                    (33)

Определение  чисел  зубьев  одиночных  передач  затруднений  не  вызывает  и  поэтому  не  рассматривается.

В  групповых  передачах,  как  правило,  модуль  зубчатого  зацепления  в  пределах  одной  множительной  группы  принимают  постоянным.  В  этом  случае  можно  записать

Z_i + Z_i' = S_z = const(34)

где  Zi  и Zi' –

соответственно         числа  зубьев  ведущего  и                  ведомого  колес  пары.

Передаточные  отношения  этих  пар  равны

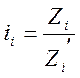                                               (35)                                        

Из  уравнений  (34)  и  (35)  получим

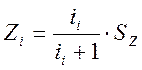                                     (36)

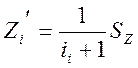                                      (37)

Определение   S_z  производится  обычно  методом  наименьшего  общего  кратного.  Положим

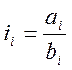                                                 (38)

где   а_i  и  b_i – взаимно  простые  числа.

Тогда 

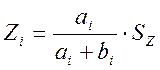                                  (39)        

Первоначально  за  величину   S_z   принимают  наименьшее  общее  кратное  величин  (а_i+b_i).  Если  при  этом  число  зубьев  меньшего  колеса  окажется  недопустимо  малым  (Z_min ≥ 18),  то  полученную  величину S_z увеличивают  в  целое  число  раз.

Рекомендуемые  значения  чисел   а_i и  b_i  для  знаменателей  φ = 1,26  и  φ = 1,41  приведены  в  таблице  5.

Таблица  5 – Рекомендуемые  значения  чисел а_i и  b_i

ii        φ	φ0	φ-1	φ-2	φ-3	φ-4	φ-5	φ-6
1,26	1/1	4/5	7/11	1/2	2/5	5/16	1/4
1,41	1/1	5/7	1/2	19/53	1/4	-	-

Для  повышающих  передач   а_i и  b_i  меняют  местами.      Пример.  Определить  числа  зубьев  для  4-х  ступенчатой  множительной  группы  со  знаменателем  φ=1,26  со  следующими  передаточными  отношениями

ii	аi/bi	(аi + bi)	Zi/Zi'
i1 = φ0	1/1	(1 + 1) = 2	27 : 27
i2 = φ-1	4/5	(4 + 5) = 9	24 : 30
i3 = φ-2	7/11	(7+11) = 18	21 : 33
i4 = φ-4	1/2	(1 + 2) = 3	18 : 36

   Наименьшим  общим  кратным  будет  18.  Наименьшее  число  зубьев  равно

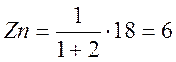
Исходя  из  условия

                               

        Имеются  таблицы  для  подбора  чисел  зубьев  зубчатых  колес  по  известным  передаточным  отношениям. Эти  таблицы  приведены  в  приложении  Б.