Методические указания для выполнения курсового проекта по дисциплине «Металлорежущие станки», страница 12

1)  1:16                       1:8                   1:4                   1:2

2)  1:8                         1:4                   1:2                   1:1

3)  1:4                         1:2                   1:1                   2:1

4)  1:2                         1:1                   2:1                   4:1

В  современных  станках  в  основном  находит  применение  2-й  вариант,  реже – 3-й.

В  результате  совместной  работе  механизмов  настройки  и  множительного,  коробка  подач  обеспечивает  получение  смешанного  арифметически-геометрического  ряда,  который  может  быть  представлен  в  виде  следующей  матрицы:

t₁₁        t₁₂        t₁₃        t₁₄                    арифметические  ряды,

                                                            пропорциональные шагу    

t₂₁        t₂₂        t₂₃        t₂₄                    нарезаемых резьб

                                                            (обеспечиваются механизмом

t₃₁        t₃₂        t₃₃        t₃₄                              настройки)

t₄₁        t₄₂        t₄₃        t₄₄                    геометрические  ряды   со  

                                                            знаменателем φ=2

(обеспечивается 

                                                             множительным механизмом)                                                                                       

Кинематический  расчет  коробок  подач  токарно-винторезных  станков  (как  и  при  всех  других  кинематических  расчетах)  заключается  в  определении  передаточных  отношений  и  чисел  зубьев  всех  звеньев  кинематической  цепи  и  проводится  в  следующей  последовательности.  В  соответствии  с  расчетными  перемещениями.

1об.заг → t,  мм

составляется  уравнение  кинематического  баланса  в  общем  виде

1 ^.  i_з ^. i_n1 ^.  i_r ^. i_n2 ^. i_н ^. i_nз  ^. i_н  ^. k_в ^. t_в =  k_н ^. t_н             (44)

где   kв,  kн –	соответственно  число  заходов  ходового  винта  и  нарезаемой   резьбы;
tв,  tн  –	передаточное    отношение     соответствующих       механизмов  настройки  и  постоянных  передач.
ti  –	передаточное    отношение     соответствующих       механизмов  настройки  и  постоянных  передач.

В  левой  части  уравнения  (44)  девять  неизвестных  величин.  Составить  дополнительные  уравнения  не  представляется  возможным,  что  исключает  однозначное  решение  этого  уравнения.  Однако,  опираясь  на  имеющийся  опыт  проектирования  токарно-винторезных  станков  и  анализируя  результаты  различных  вариантов  решения,  удается  в  итоге  получить  такое  решение,  которое  отвечает  требованиям  практики.

Все  без  исключения  токарно-винторезные  станки  не  позволяют  нарезать  резьбы  во  всем  диапазоне  шагов.  Поэтому  перед  началом  расчета  составляют  таблицу  нарезаемых  резьб  так,  чтобы  шаги  резьб  (количество  ниток  на  1'')  в  строках  располагались  по  арифметическому  ряду,  а  в  столбцах – по  геометрическому.  Модульные  и  питчевые  резьбы  обычно  в  таблицу  не  включают,  так  как  модули  нарезаемой  резьбы  численно  равны  шагам  метрической  резьбы,  а  диаметральные  питчи – количеству  ниток  на  1''.

Дальнейшие  расчеты  выполним  параллельно  с  решением  конкретного  примера.  Пусть,  например,   требуется  спроектировать  коробку  подач,  позволяющую  нарезать  метрическую  резьбу  с  шагами  0,5…7  мм,  дюймовую  с  количеством  ниток  на  1''  (4…56).  Составим  таблицу 5  нарезаемых  резьб.

Таблица 5 – Величины нарезаемых резьб

Резьба
Метрическая				Дюймовая
Шаг,  мм				Количество  ниток  на  1''
0,5	-	0,75	-	32	40	48	56
1,0	1,25	1,50	1,75	16	20	24	28
2,0	2,5	3,0	3,5	8	10	12	14
4,0	5,0	6,0	7,0	4	5	6	7

Примечание:  знак « – »  означает  нестандартный  шаг  резьбы.

Расчет  начинают  с  определения  передаточных  отношений  механизма  настройки.  При  этом  выбирают  такую  строку,  в  которой  численные  значения  для  разных  типов  резьб  были  равными  или  кратными.  Выбираем  4-ю  строку  и  принимаем  К_н = 1.

Для  получения  резьб  этой  строки  передаточные  отношения  всех  элементов  кинематической  цепи,  кроме  механизма  настройки  i_н,  должен  быть  постоянным.  Обозначим  их  буквой  «С».  Тогда  уравнение  (44)  примет  вид

                                          (45)

Отсюда

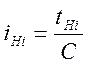                                              (46)

Величину  «С»  выбирают  таким  образом,  чтобы  одно  из  передаточных  отношений  в  средней  части  ряда  было  равным  1.  Принимаем  С = 5.

Передаточные  отношения  и  числа  зубьев  зубчатых  колес  определим  для  двух  видов  механизма  настройки.

Для  механизма  Нортона

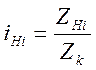
где Zнi –	число  зубьев  i-го  колеса  ступенчатого  конуса  зубчатых  колес;
Zk –	число   зубьев  подвижной  каретки  (Zk ≥ 28).

Принимаем  число  зубьев  подвижной  каретки  Z_k = 30.

Тогда,  подставляя  из  таблицы  значения i_нi,  получим

;                       ;

;                      

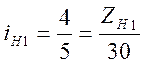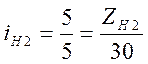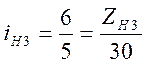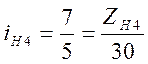
Отсюда  числа  зубьев  зубчатых  колес  ступенчатого  конуса  равны

Z_нi = 24,  30,  36,  42

Для  подвижных  блоков  зубчатых  колес  используя  выражение  (35),  получим

;             ;

;            

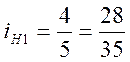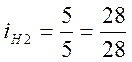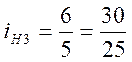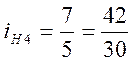
Определяя   сумму   чисел  зубьев  как  наименьшее  общее  кратное  (а_i + b_i)  получаем   недопустимо   большое   значение   этой    величины      (S_z = 396).  Поэтому  числа  зубьев  в  приведенном  решении  приняты  исходя  из  условия

Szi	55; 56	63	72
mi	2	1,75	1,5
Ai	110	110	108