Методические указания для выполнения курсового проекта по дисциплине «Металлорежущие станки», страница 6

Основная – это множительная  группа,  которой  кинематически  предшествуют  только  постоянные  передачи.

Характеристика  этой  группы

Х_о = 1                                                 (16)

Первая  переборная – это  множительная  группа,  которой  кинематически  предшествует  основная  множительная  группа.  Характеристика  этой  группы  равна  количеству  ступеней  в  основной  множительной  группе,  т.е.

Х₁ = Z_о                                                 (17)

Вторая  переборная – это  множительная  группа,  которой  кинематически  предшествуют  основная  и первая  переборная  множительная  группы.  Общее  количество  ступеней  в  предшествующих  группах  равно  Z_o^.Z₁.

Следовательно,  характеристика  этой  группы  равна

Х₂ = Z_o^.Z₁                                          (18)

Аналогично  определяют  названия  и  характеристики  последующих  множительных  групп.

Знаменатель  геометрического  ряда  i-ой  множительной  группы  равен

φ_i = φ^xi                                                (19)

где   φi –	знаменатель  геометрического  ряда  i-ой множительной  группы;
φ –	знаменатель    на    выходном    валу    сложной    коробки   скоростей    (подач);
Хi –	характеристика  i-ой  множительной  группы.

Диапазон  регулирования  i-ой  множительной  группы  равен 

                                (20)

Кинематические  функции,  выполняемые  множительными  группами,  не  зависят  от  конструктивного  порядка  их  расположения.  Так,  например,  кинематическая  группа,  стоящая  в  приводе  первой  может  выполнять  функции  последней  переборной.

Конструктивный  порядок  расположения  и  кинематический  порядок  распределения  отражаются  формулой  структуры  привода

                           (21)

При  этом  последовательность  Z_i  отражает  конструктивный  порядок  расположения,  а  значения  X_i –кинематический  порядок  распределения.

Виды  кинематических  структур  и  их  характеристика.

Нормальная  равномерная  структура – это  структура,  у  которой  характеристики  всех  множительных  групп  равны  своим  расчетным  значениям.  Совпадение  конструктивного  порядка  расположения  с  кинематическим  порядком  распределения  необязательно.  Если  передаточные  отношения  всех  передач  во  множительных  группах  приняты  в  соответствии  с  выражением  (11),  то  максимальное  значение  диапазона  регулирования  этой  структуры  будет  равно:

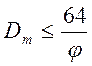                                             (22)

Такое  значение  диапазона  регулирования  может  быть  получено,  если  последняя  переборная  группа  имеет  две  ступени.  При  увеличении  количества  ступеней  в  последней  переборной  группе  диапазон  регулирования  уменьшается.

Нормальная  равномерная  структура  (как  наиболее  простая)  является  предпочтительной.  Вместе  с  тем,  диапазон  регулирования  такой  структуры  не  всегда  достаточен.  Поэтому  для  увеличения  диапазона  регулирования  применяют  структуры,  отклоняющиеся  от  нормальной  равномерной  структуры  (специальные  структуры).

Структура  с  повторением  (перекрытием)  части  ступеней.  Такую  структуру  получают  путем  присоединения  к  приводу  с  нормальной  равномерной  структурой  еще  одной  множительной  группы  из  двух  передач,  характеристика  которой  меньше  своего  расчетного  значения.  Диапазон  регулирования  D  этой  структуры  равен

D = D_m^.D_n                                         (23)

где   Dm –	диапазон    регулирования    привода    с   нормальной  равномерной структурой;
Dn –	диапазон  регулирования  присоединенной  множительной  группы

Таким  образом,  диапазон  регулирования  привода  с  нормальной  равномерной  структурой  увеличивается  в  D_n  раз.  К  приводу  можно  присоединять  не  одну,  а  несколько  множительных   групп  с  пониженным  значением  характеристик.  При  этом  диапазоны  регулирования  основного  привода  и  присоединяемых  множительных  групп  должны  быть  назначены  согласно  выражениям  (22)  и  (20).

Расчетное  количество  ступеней  структуры  с  повторением  определяется  согласно  выражению  (14).  Действительное  (рабочее)  количество  ступеней  меньше  расчетного  на  величину  DZ₁,  которая  находится  из  соотношения

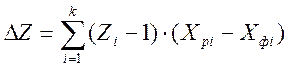             (24)

где Zi –	количество    ступеней   в   i-ой    присоединяемой    множительной группе;
Xpi –	расчетное  значение  характеристики;
Xфi –	фактическое  (принятое)  значение  характеристики;
k  –	количество   множительных   групп   со   сниженным    значением  характеристик.

Структура с  ломанным  геометрическим  рядом.  У  таких  структур  в  центре  ряда  имеется  U + 1   степень  со  знаменателем  φ₁,  а  на  границах  ряда  ступени  со  знаменателем  φ₂ .

Для  получения  ломанного  ряда, к  приводу  с  нормальной  равномерной  структурой  и  знаменателем  φ₂  присоединяют  еще  одну  множительную  группу  из  двух  передач  с  характеристикой  «Х»  по  отношению  к  знаменателю  φ₂.  Получаемые  таким  образом  ряды  всегда  симметричны.  Диапазон  регулирования  равен

                                       (25)

Значения  «Х»  находят  из  соотношения

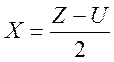                                          (26)

где  Z – общее  количество  ступеней  в  приводе.

Структуры  с  ломанным  геометрическим  рядом  позволяют  увеличить  диапазон  регулирования  привода  с  нормальной  равномерной  структурой  в    раз.

Ломанный  геометрический  ряд  возможен  не  для  всех  значений  φ,  а  лишь  для  тех,  у которых  может  быть  выдержано  соотношение:  .

При   получается  равномерный  геометрический  ряд  со  знаменателем  φ₁,  при  U=0 – со  знаменателем  .

Структуры  с  повторением  и  с  ломанным  геометрическим  рядом  имеют  такой  же  вид  формулы  структуры  привода,  что  и  нормальная  равномерная  структура.