Общие понятия и определения в математическом моделировании. Алгоритм построения математических моделей электромеханических объектов, страница 9

                                ⎧⎪⎨⎪⎪ΔτΔ≤τ ≤1 ⋅12T⋅BTTЯ_Я= =0,50,⋅5τ,В.

                                                                  ⎪⎩        2 T_Я

Пусть в результате расчетов параметров получены следующие значения:  k_Я^О = 3,485,  ^UЯN =1,301,  τ_В = 0,456,  τ_ЭМ = 2,251_,  ^IКЗ = 4,536.

                                           EЯN                                                                                                 IЯN

Выберем интервал и шаг расчета

                             τ_ПП = (5 ÷10)⋅τ_ЭМ = (5 ÷10)⋅2,251=15, 

                                     .

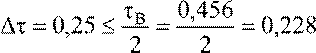Рассчитаем переходной процесс в модели, используя встроенную функцию MathCAD – rkfixed. Документ MathCAD приведен на рис. 6.1 и 6.2.

Параметры якоря 

                       k_Я := 3,485       k_Я :=1,301 τ_B := 0,456 τ_ЭМ := 2,251       i_КЗ := 4,53

Определение функции sign 

                                               sign(x) := if (x = 0,0,if (x > 0,1,-1)).

Определение функции-матрицы правых частей уравнений

                                            ⎢                                            ⎥

                                            ⎢                                            ⎥        y₀ −ток якоря

                                              kЯ ⋅(uЯ − y1 ⋅ y2) − y0                  ⎥                                                  

                                   ⎢

                         D(t, y) := ⎢_⎢ 1 ⋅(1− y₁                                             ⎥          y1 −токвозбуждения

                                                                  _{)                          ⎥}

                                            ⎢τ_B                                                                  ⎥

                                            ⎢      1                                    ⎥          y2 −угловаяскорость

                                            ⎢ ⋅(y₀ ⋅ y₁ − sign(y₂))⎥

                                            ⎣τЭМ ⋅kЯ                                                     ⎦

Задание интервала и шага расчёта

t

                                             t₀ := 0      t₁ :=15 Δτ= 0,25       N := ¹

Δτ

Задание начальных условий

⎡iКЗ⎤

⎢ ⎥

⎢ ⎥

                                                                    y₀ := _⎢ 0 _⎥

⎢ ⎥

⎢⎣ 0 ⎥⎦

Расчёт

                                                       S := rkfixed(y₀,t₀,t₁, N, D)

Перенос результатов в матрицы-столобцы

                                 τ := S<0>             iЯ := S<1>               iB := S<2>                ω:= S<3>

Значение в конце интервала расчёта

                                             i_ЯN =1,003          i_BN =1          ω_N =1,013

Рис. 6.1. Фрагмент документа MathCAD (расчет)

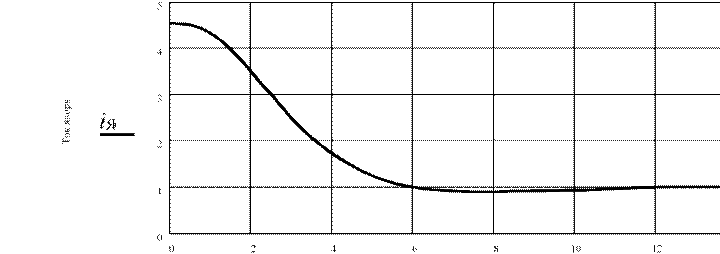
Диаграммы изменения переменных

τ

Относительное время

τ

τ

                                                                                                     Относительное время                                                                    

Рис. 6.2. Фрагмент документа MathCAD (диаграммы)

7.  Анализ полученных результатов  моделирования

Целью анализа рассчитанных переходных процессов является определение их соответствия физическим процессам, происходящим в ДПТ НВ.

При анализе рассматривают три основных момента: начало, установившиеся значения и характер переходного процесса.

Исходное (начало) и новое (установившийся режим) состояние ДПТ НВ наиболее просто установить по законам Кирхгофа, Ампера и Фарадея, которые для установившихся режимов аналитически описыd

ваются уравнениями (3.1), (3.2) при  = 0. dt

⎧UЯ = IЯ ⋅ RЯ + EЯ,

⎪

UВ = IВ ⋅ RB,

⎪⎪

                                      ⎨M_ЭМ = M_СТ ⋅sign(ω),                

⎪⎪EЯ = KE ⋅ KФN ⋅WB ⋅ IB ⋅ω,

⎪⎩MЭМ = KE ⋅ KФN ⋅WB ⋅ IB ⋅ IЯ.

В относительных величинах эта система примет вид

                                                            ⎧      О          1      О           О

                                                           ⎪⎪ UЯ = kЯO ⋅ IЯ + EЯ ,

⎪UВО = IВО,

⎪

⎪

                                         ⎨ МЭМО = МСТ0 ⋅sign(ω0),                           (7.1)

⎪