Общие понятия и определения в математическом моделировании. Алгоритм построения математических моделей электромеханических объектов, страница 6

⎧⎪ p⋅ I_Я(p) = K_Я^О ⋅[U_Я(p) − I_В(p) − ω(p)]− I_Я(p),

⎪

                                ⎪                  1

                      ⎨p⋅ I_В(p) =  ⋅[U_B(p) − I_B(p)],                                (5.1)

                                ⎪                 τВ

^⎪⎩⎪ p⋅ω(p) = τЭМ¹⋅ KЯО ⋅[I_B(p) + I_Я(p) − М_СТ(p)].

Преобразуем эту математическую модель, уже записанную  в операторной форме, к виду, удобному для изображения её в дальнейшем виде структурной схемы.

Для этого решим (5.1) относительно неизвестных величин 

⎧⎪ I_Я(p) = ^KЯО ⋅[^U_Я(p) − ^I_B(p) − ω(p)],

                                 ⎪              р +1

                                 ⎪                  1

                       ⎨I_В(p) =  ⋅U_B(p),                                          (5.2)

                                 ⎪            τ_В ⋅ p +1

^⎪⎪⎩ω(p) = τЭМ ⋅¹KЯ ⋅ p ⋅[I_B(p) + I_Я(p) − М_СТ(p)]. _О

Внимание! Линеаризованная и записанная в операторном виде через приращения относительных переменных математическая модель (5.2) пригодна только для исследования динамики электродвигателя постоянного тока независимого возбуждения «в малом». Это не следует забывать!

5.2.  Изображение операторной математической  модели в виде структурной схемы 

Математическую модель (5.2) можно условно графически представить в виде структурной схемы, которая изображается в виде прямоугольников с записанными внутри их передаточными функциями, соединённых стрелками, показывающими направление передачи информации или прохождения сигналов (переменных величин).

Передаточная функция – это отношение операторного изображения выходной величины изображения выходной величины (сигнала) какоголибо элемента матмодели к операторному изображению выходной величины

Х^ВЫХ(p).

                                                W(p) =

Х_ВХ(р)

В связи с этим определением графическое изображение 

(рис. 5.1) означает аналитическую операцию масштабирования Х_ВЫХ(р) =W(p)⋅ ^Х_ВХ(р).

                                                    XXВХВХ(p( ))p    W(p) XXВЫХВЫХ(( )pp)

Рис. 5.1

Кроме этого, в структурных схемах используются знаки суммирования (рис. 5.2) ^Х_ВЫХ(р) = ±^Х_ВХ1 ± ^Х_ВХ2(p)

                                                       XX^ВХВХ¹1(( )pp)±± XX^ВЫХВЫХ(( )pp)

±±

XXВХВХ22( )(pp)

Рис. 5.2

И знаки (точки) съёма информации (рис. 5.3)

Рис. 5.3

Учитывая это, представим матмодель (5.2) в виде структурной схемы (рис. 5.4)

Рис. 5.4. Матмодель (5.2) в виде структурной схемы 

На структурной схеме в прямоугольниках записаны относительное придаточные функции якорной обмотки ⎛⎜_⎜⎝ ^KЯО₁⎞⎟обмотки возбуж-

_{p + ⎟⎠}

                    ⎛      1       ⎞

дения ⎜⎜⎝ τ_Я ⋅ p +1⎟⎟⎠ и электромеханической части электродвигателя 

⎛         1          ⎞

⎜⎜⎝ KЯО ⋅τЭМ ⋅ p ⎟⎟⎠.

Следует обратить внимание на то, что:

1.  Все известные (заданные) величины «входят « в структурную схему (стрелки внутрь).

2.  Все неизвестные (определяемые) величины «выходят «из структурной схемы (стрелки наружу). 

3.  Внутри структурной схемы нет «разрывов» между стрелками.

Эти признаки определяют правильность построения структурной схемы!

5.3.  Правила структурных преобразований 

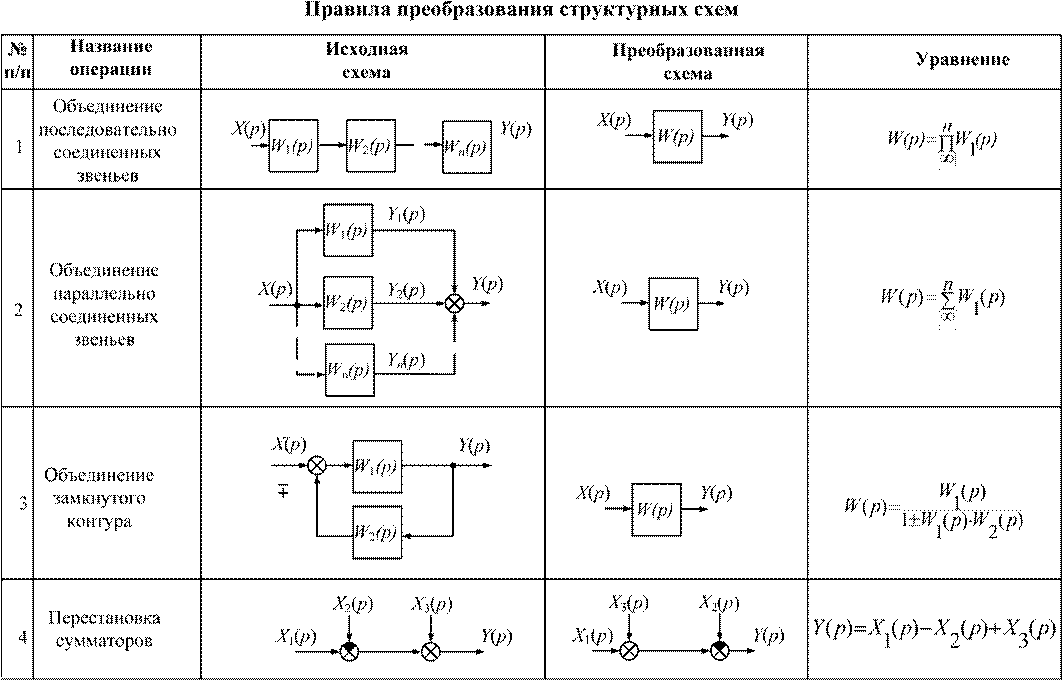
Структурные матмодели (схемы) также как и аналитические можно преобразовывать, не нарушая правил математических операций. Основной задачей структурных преобразований является упрощение структурных схем.

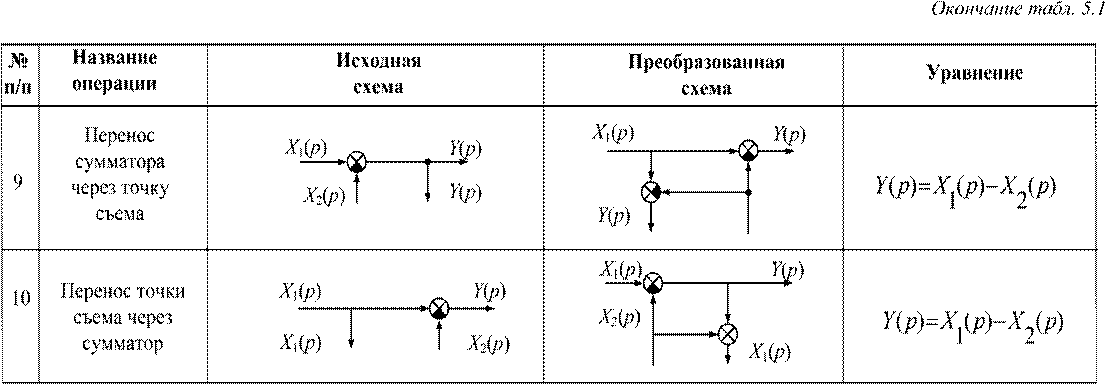
Эти преобразования производятся на основании правил, изложенных в таблице 5.1.

Покажем, как ими пользоваться, на примере структурной схемы на рис. 5.4 для случая, когда U_Я – var, U_В – const, M_СТ – const. Выходной величиной будем считать ω− var. Поскольку структурная схема представлена для приращения переменных, то в рассматриваемом случае U_Я(р) ≠ 0, ω(p) ≠ 0 , U_В(р) = 0, M_СТ(р) = 0 и схема принимает вид, представленный на рис. 5.2. 

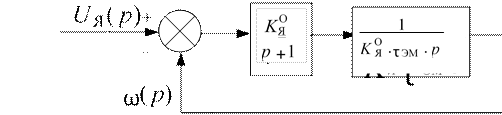
Рис. 5.5. Структурная схема управления ДПТ НВ 

по каналу U_Я(p) →ω(p)