Общие понятия и определения в математическом моделировании. Алгоритм построения математических моделей электромеханических объектов, страница 2

В связи со сказанным, математические модели электромеханических объектов (ЭМО) предлагается создавать по следующему алгоритму: а) ЭМО мысленно разделяется на основные составляющие части: электрическую, магнитную, механическую и дополнительные: гидравлическую или пневматическую, тепловую, оптикомеханическую, радиотехническую, и т. д.; б) составляются схемы замещения каждой из частей, для чего:

–  вводят упрощения за счёт неучёта второстепенных физических эффектов;

–  определяют входные, выходные и возмущающие переменные;

–  задают начало и положительные направления отсчёта всех рассматриваемых переменных; в) составляют по схемам замещения системы дифференциальных алгебраических уравнений равновесия и непрерывности по основным законам физики.

Для электрической схемы уравнения записываются по первому закону Кирхгофа: сумма электрических токов в узле равняется нулю (непрерывность) и второму закону Кирхгофа: сумма электродвижущих сил и падений напряжений в контуре равна нулю (равновесие).

Для магнитной схемы используются аналогичные законы для магнитных потоков, магнитодвижущих сил и падений магнитных напряжений.

Для механической схемы применяют принцип Даламбера для скоростей (непрерывность) и третий закон Ньютона для сил (равновесие).

Аналогичные законы имеются для пневматической (гидравлической), тепловой и других частей (законы Бернулли, Навье-Стокса и т. д.); 

г) полученную в предыдущем пункте математическую модель  в виде системы дифференциально-алгебраических уравнений преобразуют к виду, удобному для аналитического или численного исследования.

3.  Математическая модель электродвигателя постоянного тока независимого возбуждения

Проиллюстрируем использование алгоритма построения математических моделей электромеханических объектов на примере электродвигателя постоянного тока независимого возбуждения.

3.1.  Конструкция и принцип действия  электродвигателя постоянного тока

Как известно, электродвигатель постоянного тока состоит из двух основных частей: неподвижной, называемой индуктором, и вращающейся, называемой якорем.

Индуктор состоит из стального полого цилиндрического ярма,  к которому изнутри прикреплены стальные полюса с обмоткой возбуждения. Обмотка возбуждения при протекании по ней тока создает основной магнитный поток электродвигателя.

Якорь состоит из цилиндрического сердечника, собранного из листов электротехнической стали, и закрепленной в пазах сердечника обмотки якоря.

Якорь располагается внутри индуктора в магнитном поле, создаваемом полюсами с обмоткой возбуждения. Поэтому при протекании тока по обмотке якоря возникают электромагнитные силы (по закону Ампера), которые, воздействуя на витки якорной обмотки, заставляют якорь вращаться и преодолевать момент нагрузки от рабочей машины, приложенный к валу двигателя.

3.2.  Математическая модель электродвигателя  в абсолютных переменных

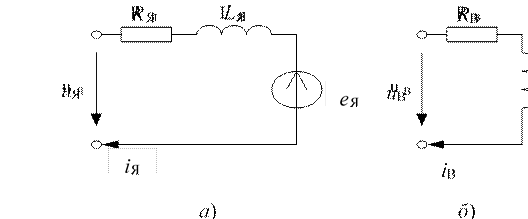
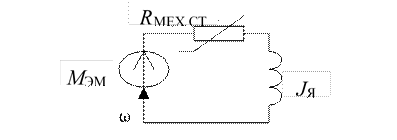
Если пренебречь потоками рассеяния, вихревыми токами, сопротивлением щеточно-коллекторного контакта, насыщением магнитной цепи, реакцией якоря, влиянием нагрева и обдува, нагрузкой демпфирования, то, в соответствии со сказанным, электродвигатель постоянного тока независимого возбуждения (ДПТ НВ) можно представить тремя упрощенными схемами замещения, изображенными  на рис. 3.1.

в)

Рис. 3.1. Схемы замещения обмотки якоря (а), обмотки  возбуждения (б) и механической части (в) ДПТ НВ

На схемах обозначено: 

u_Я, ^u_В, ⁱ_Я, ⁱ_В – напряжения и токи обмоток якоря и возбуждения;

R_Я, R_В, L_Я, L_В – активные сопротивления и индуктивности обмоток якоря и возбуждения; e_Я– ЭДС якоря, возникающая в якорной обмотке (по закону Фарадея) из-за вращения ее в магнитном поле;

M_ЭМ – электромагнитный момент, развиваемый электродвигателем (по закону Ампера) из-за наличия якорной обмотки с током в магнитном поле от обмотки возбуждения;

R_МЕХ.СТ – механическое сопротивление сухого трения, создающее постоянный (статический) нагрузочный момент М_СТ, не зависящий от угловой скорости ω якоря; J_Я – момент инерции якоря.