Тригери, тригерні схеми (RS-тригери. Загальна характеристика тригерних схем. D-тригери. JK-тригери. Т- та ТV-тригери)

Розділ IV

ТРИГЕРИ. ТРИГЕРНІ СХЕМИ

До цього часу ми розглядали цифрові схеми, в яких мав місце односторонній зв’язок від входу до виходу.

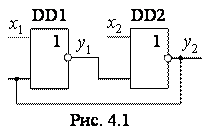Розглянемо тепер одну з найпростіших схем, в якій маємо зворотній зв’язок з виходу на вхід (рис. 4.1). Приведена схема навіть за зовнішнім виглядом має деякі  особливості:

·  По-перше, ми не можемо говорити про один вихід, так як елементи об’єднані в кільце і виходів буде стільки, скільки елементів.

·  По-друге, задавши традиційно повний перебір вхідних значень змінних х₁,х₂, побачимо, що проаналізувати стан схеми неможливо без допоміжних умов, які необхідно задавати заздалегідь.

·  По-третє, схема має позитивний зворотній зв’язок, подібно до генераторних схем, наслідком чого є те, що зміна станів окремих елементів відбувається майже одночасно для всіх елементів.

В цифровій схемотехніці такі схеми називаються тригерними схемами, або частіше просто тригерами. В загальному вигляді тригерна система має вигляд, що відповідає рис. 4.2.

В цифрових пристроях використовується велика кількість різноманітних тригерів, але всі вони мають в своєму складі елемент пам’яті (ЕП) та систему керування (СК). СК має два виходи – прямий Qта інверсний , які приймають значення 1 або 0. Керування елементом пам’яті відбувається за входами S (Set – установлення стану Q= 1, ) та R (Reset – повернення до початкового стану Q=0, ). Логічні значення сигналів  залежать від значень вхідних логічних змінних х₁ ... х_n, сигналів синхронізації c₁... c_n, станів виходів елемента пам’яті Qта  і логіки роботи схеми керування. В залежності від призначення схеми змінюється логічна функція схеми керування, кількість входів x_n, кількість і характер входів синхронізації.

В зарубіжній інженерній практиці всі тригерні схеми розділяються на дві групи. Перша з них – flip-flop – характеризується тим, що вибірка вхідних сигналів і відповідна зміна виходів визначається в моменти дії тактових часових сигналів (синхронні тригери). Особливість другої групи схем – latch – полягає в тому, що вони змінюють свій стан при появі вхідних сигналів і незалежно від наявності чи відсутності часових тактових сигналів. 

Розглянемо схеми тригерних систем на конкретних прикладах тригерів.

4.1. RS-тригери

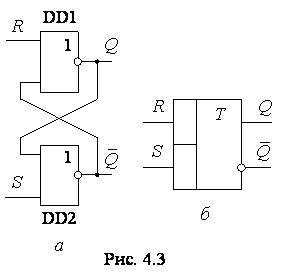Схема RS-тригера, зібраного на логічних елементах 2АБО-НІ, приведена на рис. 4.3, а. Вона відрізняється від схеми, приведеної на рис. 4.1, тільки позначеннями входів та виходів.

Завдяки симетричному вигляду, вона часто називається симетричним RS-тригером (але симетрія вигляду не означає симетрію електричних режимів роботи логічних елементів  DD1, DD2). На рис. 4.3, б приведено його умовне позначення.

Стан тригера часто ототожнюється з сигналом на прямому виході Q – тобто тригер знаходиться в одиничному стані при Q= 1,  = 0 та в нульовому – при Q= 0,  = 1.

Особливість схеми, на відміну від комбінаційної схемотехніки, полягає в тому, що будь-який із станів є стійким при відсутності вхідних сигналів.

Дійсно, припустимо, що R = S = 0, а . В цьому випадку на виході елемента DD1 зберігатиметься значення Q= 0, що витікає з логіки роботи цього елемента. Значення Q= 0 забезпечує значення виходу  елемента DD2, тобто забезпечує нульовий стан тригера.

Припустимо, що в цьому стані на входи тригера подано комбінацію потенційних сигналів R = 0, S = 1. Тоді вихід елемента DD2 прийме значення , і, відповідно, вихід елемента DD1 прийме значення Q= 1. Тобто вказаною комбінацією вхідних сигналів ми запишемо сигнал S = 1 в тригер як один біт інформації. Змінити стан тригера в попередній можливо протилежною комбінацією вхідних сигналів, тобто задавши R = 1, S = 0. Якщо ми повторимо подачу цієї комбінації вхідних сигналів при Q= 0,  , то стан тригера не зміниться. Таким чином, стан виходів тригера в момент часу, наступний за моментом зняття вхідних сигналів, залежить не тільки від комбінації вхідних сигналів, але й від попереднього стану його виходів. Тому для аналізу схеми необхідно розділення станів входів та виходів тригера в часі. Для цього попередні стани позначаються індексом n: S_n, R_n, Q_n. Стан тригера, який одержується в результаті комбінації вхідних сигналів та значень виходів в n-й момент часу, позначається як Q_n+1, . Завдяки такому розділенню станів та вхідних сигналів в часі з’являється можливість використовувати логічні функції для запису алгоритму роботи тригерів.

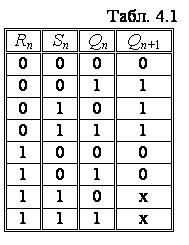Повна таблиця станів RS-тригера (Табл. 4.1) описує особливості його роботи. Звернемо увагу на те, що при S_n = R_n = 1, незалежно від Q_n, стан виходів тригера є невизначеним. Дійсно, якщо подати на обидва входи таку комбінацію сигналів, то на обох виходах з’являться логічні нулі (Q_n+1 = = 0). Але якщо ці сигнали одночасно зняти, задавши Q_n+1 = =R_n+1 = 0, то стан виходів буде невизначеним. Це пов’язано з тим, що після зняття сигналів в кожному з логічних елементів буде протікати перехідний процес зміни станів, і результат його залежатиме від швидкодії кожного з елементів. Остання є величиною невизначеною. Тому розглянута комбінація вхідних сигналів називається невизначеною комбінацією, а перехід від такої комбінації до нульової – забороненим переходом. Фактично це означає, що при проектуванні цифрових пристроїв необхідно приймати міри для виключення подібних ситуацій.

Розглянемо більш детально роботу RS-тригера з точки зору забезпечення якості та надійності переходу з одного стану в інший, адже він широко використовується в якості елемента пам’яті більш складних тригерних схем.  Подібні схеми часто називають бістабільними. Така назва витікає з того, що реально вона може знаходитись лише в одному з двох вказаних вище станів. Положення їх визначається точками перетину характеристик вхід-вихід логічних ключів, відповідно до рис. 4.5, на якому зображені характеристики вхід-вихід елементів DD1 і DD2. Точки перетину характеристик 1 і 2 є точками стабільності. Але на рис. 4.5 існує ще одна точка перетину – точка 3, яка називається метастабільною, оскільки в ній контурний коефіцієнт підсилення буде рівним 1. Положення точки 3 може бути обчислено і аналітичним шляхом, якщо існує аналітична залежність U_ВИХ = f (U_ВХ), але простіше це зробити графічно, як зображено на рис. 4.5.

Особливість метастабільної точки полягає в тому, що поява незначного шуму миттєво призведе до переходу в одну з стабільних точок, як показано стрілками на рисунку. Дійсно, поява незначного шуму на виході DD1 приведе до аналогічного зростання напруги на вході DD2 з послідуючим переходом в стабільну точку 1. Наявність метастабільної точки і необхідність її врахування в роботі цифрових схем обумовлено тим, що при незначній тривалості або амплітуді вхідних сигналів S і R схема може перейти в метастабільний стан.

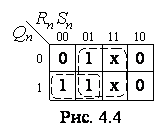
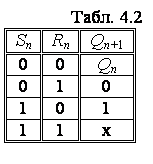Представивши Табл. 4.1 в формі карти Карно (рис. 4.4), помічаємо наступну особливість логічної функції: при значеннях S_n = R_n = 0 маємо Q_n+1 = Q_n, а для решти комбінацій входів значення виходу Q_n+1 не залежить від значення Q_n. Це дає можливість мінімізувати Табл. 4.1 (див. Табл. 4.2) та одержати характеристичне рівняння тригера:

(4.1)

Перетворюючи рівняння (4.1) в базиси логічних функцій І-НІ, одержуємо:

		(4.2)
	Цим рівнянням відповідає схема рис. 4.6. Перше з них виконане на DD1, а друге на DD2. Цей тригер працює в інверсних кодах.