Пристрої комбінаційної схемотехніки (Використання базових логічних елементів. Мультиплексори. Арифметичні пристрої. Схеми контролю)

РОЗДІЛ  ІІІ

ПРИСТРОЇ  КОМБІНАЦІЙНОЇ  СХЕМОТЕХНІКИ

3.1. Використання базових логічних елементів

Розглядаючи серії мікросхем різних технологій та різних фірм-виробників, легко встановити високий рівень уніфікації наборів типових логічних елементів та їх технічних характеристик.

Разом з однофункціональними елементами (HI, I, АБО), широко використовуються двофункціональні (I-HI, АБО-HI, ВИКЛЮЧАЮЧЕ АБО). Більш обмежено використовуються трифункціональні (I-АБО-HI) з різним рівнем розширення. Вказаний набір комбінаційних мікросхем з повного набору серії, що зветься бібліотекою, є базовим набором або базовими логічними елементами. Більш того, проектовані матричні великі інтегральні схеми (BIC) орієнтуються також на використання логічних функцій, тотожних базовим логічним елементам.

Серед задач, які часто зустрічаються при проектуванні логічних схем, слід виділити наступні:

·  реалізація функцій в базисах I-HI, АБО-HI;

·  розширення логічних можливостей елементів.

Задача реалізації логічних функцій розв’язується шляхом використання правила подвійного заперечення та теореми де Моргана. Проілюструвати це легко на наступних прикладах.

Приклад 1. Використовуючи елементи I-HI, реалізувати функцію:

(3.1)

Розв’язання. На основі правила подвійного заперечення функція (3.1) може бути зображена в вигляді:

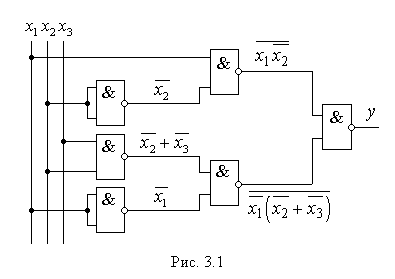
Враховуючи, що , логічну схему можемо зобразити в вигляді, приведеному на рис. 3.1.

Приклад 2. Використовуючи елементи АБО-HI, реалізувати функцію:

.

(3.2)

Розв’язання. За аналогією з попереднім прикладом, вираз зобразимо у вигляді:

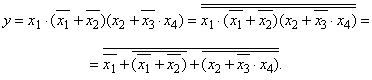
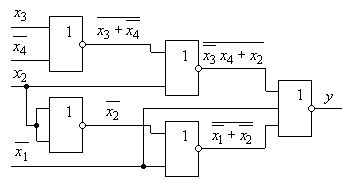
Реалізація функції (3.2) приведена на рис. 3.2.

Рис. 3.2

Вирішення задачі розширення логічних можливостей елементів розглянемо на наступних прикладах.

Приклад 3. Збільшити коефіцієнт розгалуження по виходу К_р на величину, перевершуючу значення стандартного елемента.

Розв’язання. В залежності від величини необхідного коефіцієнта розгалуження, використовуються три варіанти схем, приведені на рис. 3.3, а, б, в.

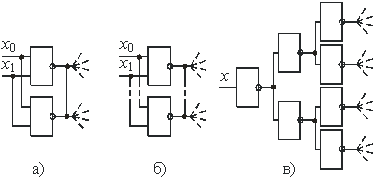      Рис. 3.3

Перший з можливих варіантів – запаралелення двох елементів (рис. 3.3, a). Така схема підвищення потужності виходу ТТЛ-мікросхем використовується лише для двох мікросхем, що знаходяться в одному корпусі. Підвищення кількості мікросхем приведе до появи вирівнюючих струмів. В КМОН-серіях такого обмеження принципово немає, але слід пам’ятати, що зростання кількості запаралелених елементів приводитиме до росту величини вихідної паразитної ємності.

Схема, приведена на рис. 3.3, б, за кількістю елементів для КМОН IC також не має обмежень, а для ТТЛ обмеження задається потужністю джерел сигналів x₀ та x₁.

Схема рис. 3.3, в каскадного розмноження кількості виходів фактично не має ніяких обмежень і використовується в схемах при розводці кіл синхронізації.

Приклад 4. Використовуючи елементи ТТЛ IC, розробити схему I на 9 входів.

Розв’язання. В серіях ТТЛ використовуються багатовходові елементи I 4(2I), 3(3I), 2(4I), а також елементи 2I-НІ – 2(4I-HI), 1(8I-HI), 3(3I-HI) (позначення 2(4І-НІ) говорить про те, що в одному корпусі мікросхеми наявні два чотиривходові логічні елементи).

При використанні елементів 3(3I) (наприклад, мікросхеми K555ЛІ3 (зарубіжні аналоги – 74LS11, 74LS11N, DL011D, UCY74LS11N)) використовується каскадне з’єднання елементів.

При використанні елементів 3(3I-HI) логічну функцію:

перетворимо до виду:

(3.3)

З (3.3) витікає, що необхідна схема може бути створена на базі мікросхеми 3(3I-HI) (K1533ЛA4), виходи яких об’єднуються елементом 3(АБО-HI) (K1533ЛE4).

Приклад 5. Використовуючи елементи ТТЛ IC, розробити схему на 9 входів АБО.

Розв’язання. В серіях ТТЛ використовуються мікросхеми 4(2АБО-HI) (TD3402, 5402DM, 5402FM, 7402DC,7402FC, SW7402N, T7428B1, SN8426N), 3(3АБО-HI) (5427DM, 5427FM, 7427DC, 7427PC, SN7427N), 2(5АБО-НІ).

При використанні елементів 3(3АБО-HI) логічну функцію:

перетворимо до виду:

(3.4)

Функцію (3.4) на практиці можна реалізувати шляхом використання трьох елементів 3АБО-HI (мікросхема К1533ЛЕ4 (зарубіжні аналоги – 7427PC, DM7427N, ECG7427, MC7427N, SN7427N)), виходи яких об’єднуються одним елементом 3I-HI (K1533ЛА4).

Приклад 6. Побудувати схему знаходження суми по модулю 2 на вісім входів, використовуючи двовходовий елемент ТТЛ.

Розв’язання. В серіях ТТЛ використовуються мікросхеми з двома входами К555ЛП5 (зарубіжні аналоги – 74LS86N, SN74LS86J), КР1533ЛП5 (аналог – 74ALS86) та К555ЛЛ3 (вихід останньої – з відкритим колектором). Вони реалізують наступну логічну функцію:

.

Логічна функція, реалізацію якої поставлено задачею, має вигляд:

.

(3.5)

Для побудови схеми, що реалізує функцію (3.5), скористаємось сполучним законом, завдяки якому виконаємо два варіанти перетворень:

;	(3.6)
	(3.7)

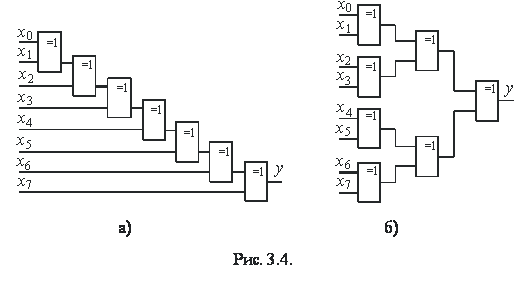
Формула (3.6) дає можливість створити послідовну схему (рис. 3.4, a); (3.7) – відповідно, пірамідальну (рис. 3.4, б). Обидві схеми по апаратних затратах еквівалентні і виконуються з використанням двох корпусів, наприклад, мікросхеми К555ЛП5. Але величини часових затримок в них суттєво різні.

В першому випадку величина затримки виконання операції t₃ пов’язана з затримкою елемента t₃₀ та їх кількістю m співвідношенням:

.

При пірамідальному з’єднанні величина t₃ суттєво менша і знаходиться по формулі:

.

Перша з розглянутих схем (рис. 3.4) використовується, наприклад, для виділення фронту та спаду імпульсу, а також для подвоєння частоти імпульсів.

Ці властивості ілюструються схемою та часовими діаграмами, що приведені на рис. 3.5, a, б. Елементи DD1.1 – DD1.3 виконують затримку імпульсу U_ВХ на величину t₃ = 3 t₃₀, а DD1.4 виділяє імпульси U_ВИХ відповідно до логіки роботи елемента.

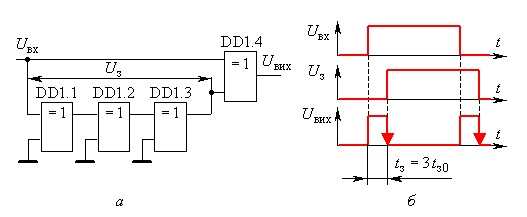
Рис. 3.5

Схема, приведена на рис. 3.4, б, є основою схем, призначених для перевірки на парність багаторозрядних цифрових слів (наприклад, мікросхеми К1533ІП2 (зарубіжні аналоги – 74180PC, CDB4180E, SN74180N, UCY74180N) та К561СA1 (зарубіжні аналоги – 4531BDC, 4531BDM, 4531BFC, 4531BFM, 4531BPC, GD4531BC, GD4531BDC, GD4531BDM)), які широко використовуються в комп’ютерній техніці.

Приклад 7. Використовуючи елементи ВИКЛЮЧАЮЧЕ АБО, розробити схему пристрою для вмикання (вимикання) освітлення в приміщенні з трьома входами, біля кожного з яких повинен розміщуватись вимикач.

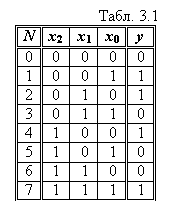Розв’язання. Складаємо таблицю станів функції, що реалізується пристроєм, прийнявши за логічні змінні стани вимикачів – відповідно x₂, x₁, x₀ (Табл. 3.1).

 Прийнявши, що при вимкнених вимикачах лампочка освітлення не горить, тобто y = 0 при x₀ = 0, x₁ = 0, x₂ = 0, істинні значення функції будуть лише при непарній кількості ввімкнених вимикачів, тобто для мінтермів з порядковими номерами 1, 2, 4, 7.

Логічна функція буде описуватись наступним виразом:

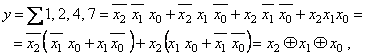
оскільки

.

Схема пристрою може бути реалізована по одному з двох варіантів, приведених на рис. 3.4, а, б.