Найпростішим перетворювачем можна вважати схему, що, незалежно від коду, який подається на її вхід (прямий чи зворотній), на виході завжди видає прямий код (рис. 3.14).
Схема в кожному біті перетворювача реалізує операцію:
![]() ,
,
в зв’язку з чим при наявності в знаковому розряді х4 одиниці (від’ємне число) код порозрядно інвертується, а при х4 = 0 передається без змін. В багатьох серіях такий перетворювач може бути реалізованим на мікросхемі ЛП5.
В розглянутому випадку відповідність між вхідним та вихідним кодами задається формулою. Але частіше необхідна формула одержується з таблиць відповідності кодів. Деякі з них розглядались в розділі 1.
Розглянемо декілька прикладів розробки перетворювачів кодів.
Приклад 10. Створити перетворювач двійкового коду в прямий код семисегментних індикаторів для відображення цифр десяткової системи счислення.
|
Табл. 3.3
|
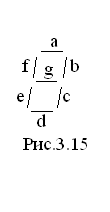
 Розв’язання. Умовне розміщення світлодіодів матриці
семисегментного індикатора приведено на рис. 3.15. Відповідно до нього
створюємо таблицю відповідності (Табл. 3.3), приписуючи значення «1» тому
світлодіодові, що засвічується при відображенні цифри, та нуль – в протилежному
випадку. Табл. 3.3 відповідає логіці роботи дешифратора К564ИД5 (зарубіжними аналогами якого є мікросхеми
4056DIE1, CD4056BD, CD4056BDF3, CD4056BE, CD4056BF, CD4056BFF3A, CD4056BH,
CD4056BK, CD4056BKF3A, HCC4056BD, HCC4056BF, HCC4056BK, HCF4056BC1, HCF4056BM,
NJU4056B, TC4056BF).
Розв’язання. Умовне розміщення світлодіодів матриці
семисегментного індикатора приведено на рис. 3.15. Відповідно до нього
створюємо таблицю відповідності (Табл. 3.3), приписуючи значення «1» тому
світлодіодові, що засвічується при відображенні цифри, та нуль – в протилежному
випадку. Табл. 3.3 відповідає логіці роботи дешифратора К564ИД5 (зарубіжними аналогами якого є мікросхеми
4056DIE1, CD4056BD, CD4056BDF3, CD4056BE, CD4056BF, CD4056BFF3A, CD4056BH,
CD4056BK, CD4056BKF3A, HCC4056BD, HCC4056BF, HCC4056BK, HCF4056BC1, HCF4056BM,
NJU4056B, TC4056BF).
З табл. 3.3 можемо записати функції роботи кожного світлодіода:

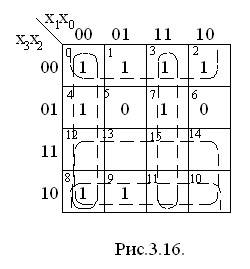
Кожна з визначених функцій може бути мінімізована з допомогою карт Карно. Наприклад, для функції b карта приведена на рис. 3.16, в якій є невизначеними 5 кліток. Довизначивши їх одиницями, після мінімізації знаходимо:
![]()
Технічна реалізація вказаної функції не має ніяких складностей.
Аналогічно можуть бути знайдені і інші функції, визначаючі роботу кожного світлодіода, та реалізовані в базисі І, АБО, НІ.
Таким чином, для побудови перетворювачів кодів перш за все необхідно створити таблицю відповідності. Таблиця відповідності фактично складається з двох таблиць. Перша з них – це таблиця перебору змінних перетворюваного коду, а друга – це таблиця відповідності змінних отримуваного коду. З приведеного вище прикладу витікає, що для створення перетворювача кожна з логічних змінних отримуваного коду повинна розглядатись як функція, в якій аргументами виступають змінні перетворюваного коду.
 В ряді
випадків при побудові перетворювачів кодів з’являються логічні функції, які
простіше реалізовувати за допомогою арифметичних обчислень.
В ряді
випадків при побудові перетворювачів кодів з’являються логічні функції, які
простіше реалізовувати за допомогою арифметичних обчислень.
Приклад 11. Розробити логічну схему перетворювача прямого двійкового коду в доповнюючий.
Розв’язання. Доповнюючий код отримується інвертуванням кожного розряду прямого двійкового коду і додаванням до отриманого результату одиниці шляхом двійкової арифметики (таблиця відповідності кодів приводиться в розділі 1).
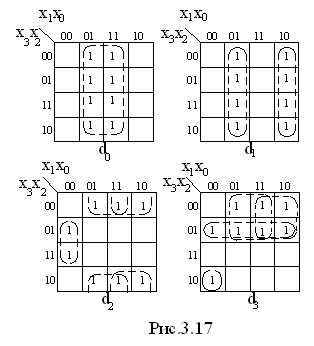
Карти Карно для вихідних функцій перетворювача прямого двійкового коду в доповнюючий приведені на рис. 3.17.
Мінімізовані значення логічних функцій:
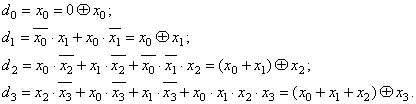
З аналізу приведених формул можна знайти загальний вигляд функції для і-го розряду вихідної функції:
![]()
Як витікає з одержаних формул, з підвищенням розрядності формула для знаходження вихідної функції dі значно ускладнюється і фактично становиться недоцільним її використання. Тому для знаходження розрядів доповнюючого коду більш економним для багаторозрядних чисел становиться перетворення їх в зворотній код з послідуючим додаванням одиниці до молодшого розряду за допомогою суматора.
Аналогічно вирішуються задачі і при проектуванні двійково-десяткових перетворювачів кодів (див. розділ 1). Наприклад, для перетворення двійково-десяткового коду в код «з надлишком 3» економніше використовувати суматор, що додає число 11 (3 – в двійковому коді) до молодших розрядів числа.
В залежності від характеру перетворення інформації, ці операції називають шифрацією або дешифрацією (широко використовується термінологія кодування та декодування). Шифрація полягає в перетворенні m-розрядного коду з km байдужих наборів вхідних змінних в однозначно відповідний йому n-розрядний код з меншим числом розрядів (n < m) і байдужих наборів. Під байдужими наборами в будь-якому коді маються на увазі ті набори, які не використовуються при перетворенні. Пристрої, які виконують вказані операції, називаються відповідно шифраторами та дешифраторами (кодерами та декодерами).
Приклад 12. Розробити схему шифратора для перетворення десяткового коду з клавіатури калькулятора в відповідний йому двійково-десятковий код.
Розв’язання. Приймемо, що при натисканні відповідної клавіші (0...9) низький рівень відповідного сигналу перетвориться в чотирирозрядний двійковий код від 0000 до 1001. Таблиця шифратора «з 10 в 4» (і, відповідно, дешифратора «з 4 в 10») приводиться нижче (Табл. 3.4).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.