При необхідності реалізувати перемножувач двох восьмирозрядних слів кожне з них розбивається на групи по 4 біти, і з кожною з груп виконуються операції, як з одною змінною, по принципу знаходження проміжної суми з послідуючим виконання операції здвигу. На базі чотирьохрозрядних перемножувачів і з використанням такої структури будується перемножувач восьмирозрядних слів.
 Контроль логічних перетворень.Розглянуті в попередніх параграфах засоби контролю правильності передачі
кодів виконують контроль лише незмінних даних. Якщо коди піддаються логічним
перетворенням, то засоби, контролюючі їх правильність, стають дуже складними.
Найпростіший спосіб контролю – це дублювання логічних перетворень та їх
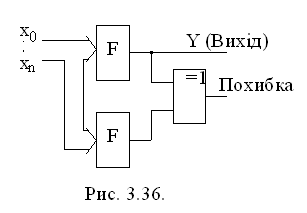
контроль (рис. 3.36). Відповідно до рисунку, логічна схема F
дублюється аналогічною схемою. Це дає можливість забезпечувати безперервний
контроль вихідного потоку інформації і в разі їх неспівпадання видавати сигнал
похибки. При такій формі контролю слід враховувати той факт, що збої в роботі
цифрової схемотехніки можуть з’являтись не тільки за рахунок дефектів схеми,
але й при наявності завад по живленню. Тому при однакових цифрових схемах
велика ймовірність появи однакових збоїв. Це значить, що дублюючі пристрої
необхідно виготовляти на різних схемах. Один з таких варіантів побудови
дублюючих схем – це використання взаємно протилежних логічних схем відповідно
до теореми де Моргана.
Контроль логічних перетворень.Розглянуті в попередніх параграфах засоби контролю правильності передачі
кодів виконують контроль лише незмінних даних. Якщо коди піддаються логічним
перетворенням, то засоби, контролюючі їх правильність, стають дуже складними.
Найпростіший спосіб контролю – це дублювання логічних перетворень та їх
контроль (рис. 3.36). Відповідно до рисунку, логічна схема F
дублюється аналогічною схемою. Це дає можливість забезпечувати безперервний
контроль вихідного потоку інформації і в разі їх неспівпадання видавати сигнал
похибки. При такій формі контролю слід враховувати той факт, що збої в роботі
цифрової схемотехніки можуть з’являтись не тільки за рахунок дефектів схеми,
але й при наявності завад по живленню. Тому при однакових цифрових схемах
велика ймовірність появи однакових збоїв. Це значить, що дублюючі пристрої
необхідно виготовляти на різних схемах. Один з таких варіантів побудови
дублюючих схем – це використання взаємно протилежних логічних схем відповідно
до теореми де Моргана.
В ряді випадків для передачі контрольованої інформації використовуються парафазнi коди, коли дублюється канал передачі інформації, i по другому каналу завжди передається сигнал, інверсний сигналу першого каналу; якщо ці сигнали в кожний тактовий момент скласти по модулю 2, то нульовий результат буде завжди говорити про наявність похибки в одному з каналів.
Комбiнацiйнi схеми, що реалізують систему булевих функцій, на відміну від одновихiдних схем, можливо контролювати, не використовуючи їх дублювання. Прикладом схеми з таким контролем приводиться на рис. 3.37.
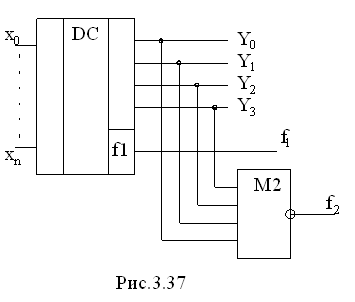 Для цього при проектуванні кодового перетворювача необхідно закласти
реалізацію ним допоміжної функції f1, яка задається як
функція аргументів, значення якої співпадають із значеннями суми по модулю 2
решти функцій. Протифазна функція f2 є
схемою контролю парності всіх функціональних виходів перетворювача, окрім f1.
Одиночна похибка в роботі як схеми перетворювача, так i схеми М2
змінить значення парності або f1, або f2
i буде зафіксована схемою контролю. Функція f1 повинна
синтезуватись з використанням вхідних змінних х0 ... хn.
Якщо ж використати для її побудови вихідні значення Y0 ...
Y3, то можливі похибки можуть змінити одночасно як f1,
так i f2 i не будуть виявлені. Вказану особливість
необхідно враховувати при розробці схем контролю більш складних перетворювачів,
в яких декілька різних виходів можуть мати загальні схемиi, відповідно,
загальні збої, які потім не можуть бути виявлені схемами типу М2.
Для цього при проектуванні кодового перетворювача необхідно закласти
реалізацію ним допоміжної функції f1, яка задається як
функція аргументів, значення якої співпадають із значеннями суми по модулю 2
решти функцій. Протифазна функція f2 є
схемою контролю парності всіх функціональних виходів перетворювача, окрім f1.
Одиночна похибка в роботі як схеми перетворювача, так i схеми М2
змінить значення парності або f1, або f2
i буде зафіксована схемою контролю. Функція f1 повинна
синтезуватись з використанням вхідних змінних х0 ... хn.
Якщо ж використати для її побудови вихідні значення Y0 ...
Y3, то можливі похибки можуть змінити одночасно як f1,
так i f2 i не будуть виявлені. Вказану особливість
необхідно враховувати при розробці схем контролю більш складних перетворювачів,
в яких декілька різних виходів можуть мати загальні схемиi, відповідно,
загальні збої, які потім не можуть бути виявлені схемами типу М2.
3.6. Перехідні процеси в логічних схемах
Відповідно до розділу 2, логічні ключі характеризуються часом затримки tЗ, який пов’язаний з перехідними процесами зміни стану. Тривалість перехідних процесів не є стабільною величиною i залежить від багатьох факторів. При використанні мікросхем ЕЗЛ, в яких внутрішні затримки малі, при проектуванні цифрових пристроїв слід обов'язково враховувати тривалість перехідних процесів в лініях зв'язку та вплив параметрів ліній зв’язку на тривалість перехідних процесів в мікросхемах. Ці задачі досить складні, i їх розв’язання можливе лише з використанням спеціальних методів моделювання.
При використанні мікросхем з тривалістю зміни станів, не меншою 20 нс (ТТЛ, КМОН), перехідні процеси в лініях зв’язку не враховуються, а характер лінії зв’язку, величина та характер навантаження враховуються максимальною тривалістю затримки. Це значно спрощує процес проектування цифрових пристроїв, адже затримки можуть бути враховані відразу на стані логічного проектування. В таких ситуаціях, коли мають місце значні затримки в лініях зв'язку, вони також можуть враховуватись як дискретні затримки.
На жаль, в паспортних даних на мікросхеми подається тільки максимальна тривалість затримки. Реально ж вона може змінюватись в широких межах, i мінімальна величина затримки паспортно не визначена. Звідси витікає, що рівень виходу елемента в цифровій схемі в інтервалі часу від 0 до tЗ не визначений. Він називається станом невизначеності i позначається символом xн. Такий стан елемента в схемі впливає на інші елементи, на виходах яких можуть мати місце як визначені стани „1”, „0”, так i невизначений стан xн. Як результат, поведінка логічних елементів в перехідних процесах описується законами трiйкової логіки зі слiдуючими логічними співвідношеннями:
|
|
|
|
 Приведені формули широко використовуються при аналізі перехідних
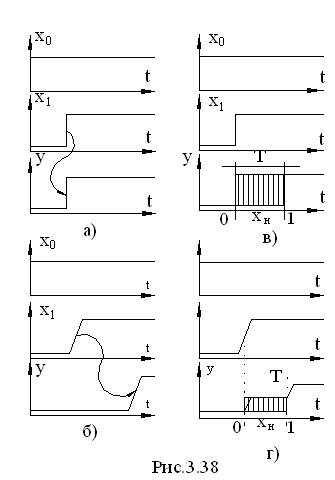
процесів, в тому числі при побудові часових діаграм. Останні зображаються одним
з двох способів, які приведені на рис. 3.38, а для елемента 2I (
Приведені формули широко використовуються при аналізі перехідних
процесів, в тому числі при побудові часових діаграм. Останні зображаються одним
з двох способів, які приведені на рис. 3.38, а для елемента 2I (![]() ).
).
В практиці аналізу схем використовуються чотири типи зображення перехідних процесів, які використовуються в залежності від необхідного рівня деталізації. Найпростіша з них – діаграма рис. 3.38, а – пояснює лише логічні зв'язки між вхідними сигналами та вихідними станами без врахування вихідних затримок. Схема рис. 3.38, б враховує часові затримки, причому їх максимальне значення. Вона дає можливість оцінити максимальні значення тривалості перехідних процесів. Інтервал t невизначеного стану xн дорівнює величині tЗконкретної мікросхеми. Лінії зі стрілками показують взаємозв'язки між вхідними сигналами i вихідними станами мікросхеми.
Діаграми рис. 3.38, в, г враховують стани невизначеності елементів. Вони дають можливість змоделювати поведінку схеми при будь-яких комбінаціях i часових співвідношеннях внутрішніх затримок.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.