При забезпеченні на входах V1 i V2 низького логічного рівня сигнали, що поступають на входи Y та Е будуть передаватись на свої виходи Y0 ... Y3 та Е0 ... Е3 в відповідності до зміни адресів. Якщо входи Y та Е об’єднати, як показано на рис. 3.23 в мікросхемах DD2, DD5, то з’єднання входів Y дасть нам можливість організувати схему демультиплексора «з 1 на 8». При забезпеченні х = 0 схема рис. 3.23. перетворюється в дешифратор «з 5 на 32». Якщо в мікросхемі DD1 об’єднати входи Y та Е для створення адресної шини а6, то при нульових сигналах на входах V1 та V2 i відповідному нарощенні вихідних мікросхем одержимо дешифратор «з 6 на 64».
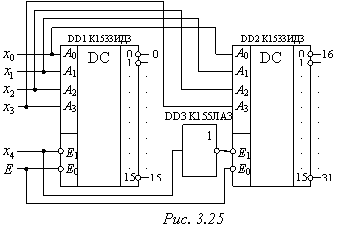Приклад 16. Використовуючи 4-розрядний дешифратор К1533ІД3 (SN74154N), розробити принципову схему дешифратора для
перетворення п’ятирозрядного коду х1 – х5
з напругою низького рівня на одному з 32 виходів.
Розв’язання. Принципова схема розробленого дешифратора приведена на рис. 3.25 (DD1, DD2 – К1533ІД3 (зарубіжний аналог – SN74154N); DD3 – К1533ЛА3 (зарубіжні аналоги – 7400PC, CDB400E, D100D, MH7400, SN7400N)).
Приклад 17. Використовуючи дешифратори серії 564ІД1, розробити принципову схему дешифрації
шестирозрядного двійкового коду на 64 виходи.
Розв’язання. Дешифратор 564ИД1 виконує перетворення 4-х розрядного двійкового коду в вихідний сигнал високого рівня на одному з 10 виходів. Із таблиці істинності мікросхеми маємо, що при зміні двійкового коду в інтервалі значень, відповідаючих десятковим числам 0 – 9, має місце однозначна відповідність вхідного двійкового коду і сигналу високого рівня на відповідному виході 0 – 9. При значеннях вхідного двійкового коду, більших 1001, виходи 0 – 7 мають нульовий вихідний сигнал. Таким чином, мікросхема дозволяє однозначно виконувати дешифрацію трьохрозрядного двійкового коду на один з 8 виходів при наявності нуля на вході А3 (рис. 3.26). При наявності сигналу високого рівня на вході А3 виходи 0 – 7 будуть відключені. Тобто вхід А3 може виконувати функцію входу, який дозволяє роботу мікросхеми з декодування інформації, яка надходить на входи А0, А1, А2.
Приведений аналіз показує, що мікросхему можна використовувати для побудови дешифратора шестирозрядного двійкового коду на 64 виходи лише шляхом їх пірамідальної побудови. Для цього 8 дешифраторів запаралелюються по входах А0 – А2, а вхід А3 підключається до виходів керуючого дешифратора через інвертори. Входи А0 – А2 керуючого дешифратора є старшими розрядами адресної шини х0 – х5.
 |
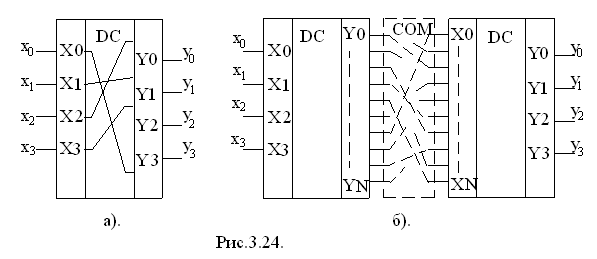На рис. 3.24 приведені 2 варіанти засекречення інформації. Спосіб перестановки з допомогою внутрішніх комутаторів (рис. 3.24, а) дає можливість для n-входового перетворювача створити n! можливих варіантів. Спосіб підстановки розширює кількість варіантів, адже перестановка виконується після перетворення вхідного двійкового коду. Кількість можливих варіантів з’єднань з допомогою комутатора СОМ підвищується до 2n! Зворотнє перетворення інформації забезпечується блоком з зворотнім законом перестановки. Використання подібних пристроїв дає можливість відкрито передавати та зберігати конфіденційну та секретну інформацію.
3.4. Арифметичні пристрої
До арифметичних пристроїв відносяться суматори, компаратори, арифметико-логічні пристрої, а також схеми для математичної обробки інформації на їх основі. В практиці цифрової схемотехніки існує декілька типів арифметичних пристроїв – наприклад, паралельного, послідовного типу, пристрої зі збереженням інформації та інші. В цьому розділі будуть розглядатись лише схеми комбінаційного типу.
Суматори. Найпростішою схемою є напівсуматор, який виконує операцію знаходження суми двох однорозрядних слів.
Табл. 3.7 Табл. 3.8
|
а0 |
b0 |
S |
P |
N |
ai |
bi |
pi-1 |
Si |
Pi+1 |
|
|
0 0 1 1 |
0 1 0 1 |
0 1 1 0 |
0 0 0 1 |
0 1 2 3 |
0 0 0 0 |
0 0 1 1 |
0 1 0 1 |
0 1 1 0 |
0 0 0 1 |
|
|
4 5 6 7 |
1 1 1 1 |
0 0 1 1 |
0 1 0 1 |
1 0 0 1 |
0 1 1 1 |
Роботу напівсуматора описує Табл. 3.7, з якої знаходимо логічні рівняння для суми і для переносу:
При знаходженні суми багаторозрядних слів напівсуматор може використовуватись лише в молодшому розряді. Для знаходження суми старших розрядів схема повинна мати три входи – два інформаційні і третій – вхід переносу з молодших розрядів. Схема, що відповідає цим вимогам, називається повним суматором, а логіку її роботи описує Табл. 3.8.
З Табл. 3.8 знаходимо наступні рівняння:
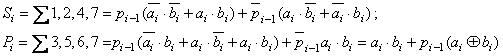
для побудови логічної схеми однорозрядного повного
суматора.
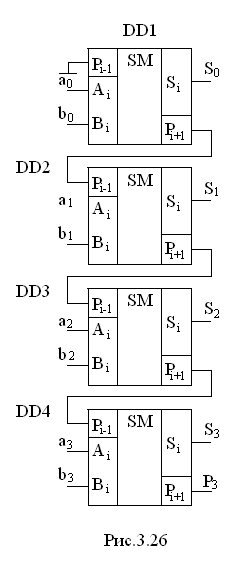
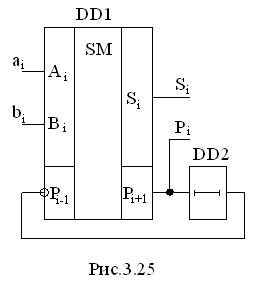Знаходження суми багаторозрядних слів може
виконуватись як послідовно, так і паралельно. Для послідовного виконання
операції використовується один повний суматор, загальний для всіх розрядів. Для
виконання операції суми слова подаються на інформаційні розряди послідовно,
починаючи з молодших розрядів (рис. 3.25).
Для врахування результату операції з попереднім розрядом вхід та вихід переносу об’єднується через елемент затримки DD2. Цей елемент повинен забезпечити затримку та зберігання сигналу pі+1 на один такт виконання операції. Синхронно з інтервалом в один такт повинні подаватись і вхідні данні аі, bі.
Приведена схема виконання операції суми сама по собі нескладна, але вимагає складного апаратного забезпечення. До того ж, послідовне порозрядне виконання операції суттєво знижує швидкодію.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.