На рис. 3.26 приведена схема організації 4-х розрядного паралельного суматора з послідовним переносом. Для кожного розряду в ній використовується окремий однорозрядний повний суматор, які з’єднані між собою послідовно по виходах-входах переносу. Незважаючи на паралельну одночасну подачу всіх розрядів слів, операція в і-му розряді починає виконуватись тільки після того, як поступить сигнал переносу з (і-1)-го розряду. Звідси витікає, що швидкодія суматора визначатиметься сумою затримок передачі сигналу переносу з молодшого розряду на вихід суматора старшого розряду.
 За схемою, приведеною на рис. 3.26,
виготовляються мікросхеми К1533ІМ3 (зарубіжні
аналоги – 7483PC, CDB483E, FJH211, FLH241, MC7483N, MIC7483N, N7483B, N7483N,
SN7482AN, SN7482N, UCY7483N),
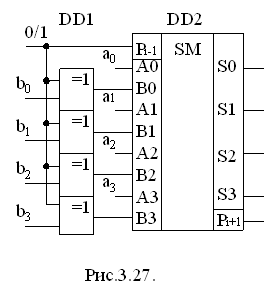
умовне зображення якої приведено на рис. 3.27 (мікросхема DD2). Мікросхема може
використовуватись для операцій як з додатніми, так і з від’ємними числами. При
виконанні операції додавання на вхід р0 необхідно
подати сигнал низького рівня. Нарощування розрядності суматорів виконується на
схемі, приведеній на рис. 3.26. Таблиця станів для суматорів за своєю сутністю
є таблицею суми двох чисел (Див. Табл. 3.7 – 3.8). Вона має простий вигляд і
зручна в користуванні для чисел невеликої розрядності. Суматор К1533ІМ3, як і
всі комбінаційні схеми, має широкі функціональні можливості. Перш за все, він
може використовуватись для знаходження суми чисел з меншою розрядністю. Схема
входів-виходів при цьому може бути різноманітною. Його можливо використовувати
і для віднімання двох чисел. Ця операція виконується шляхом додавання
зменшуваного і зменшуючого, представленого в доповнюючому коді. Для виконання
цієї операції зменшуюче b3b2b1b0
з допомогою інверторів перетворюється в зворотній код, а потім до нього по
входу р0 додається одиниця.
За схемою, приведеною на рис. 3.26,
виготовляються мікросхеми К1533ІМ3 (зарубіжні
аналоги – 7483PC, CDB483E, FJH211, FLH241, MC7483N, MIC7483N, N7483B, N7483N,
SN7482AN, SN7482N, UCY7483N),
умовне зображення якої приведено на рис. 3.27 (мікросхема DD2). Мікросхема може
використовуватись для операцій як з додатніми, так і з від’ємними числами. При
виконанні операції додавання на вхід р0 необхідно
подати сигнал низького рівня. Нарощування розрядності суматорів виконується на
схемі, приведеній на рис. 3.26. Таблиця станів для суматорів за своєю сутністю
є таблицею суми двох чисел (Див. Табл. 3.7 – 3.8). Вона має простий вигляд і
зручна в користуванні для чисел невеликої розрядності. Суматор К1533ІМ3, як і
всі комбінаційні схеми, має широкі функціональні можливості. Перш за все, він
може використовуватись для знаходження суми чисел з меншою розрядністю. Схема
входів-виходів при цьому може бути різноманітною. Його можливо використовувати
і для віднімання двох чисел. Ця операція виконується шляхом додавання
зменшуваного і зменшуючого, представленого в доповнюючому коді. Для виконання
цієї операції зменшуюче b3b2b1b0
з допомогою інверторів перетворюється в зворотній код, а потім до нього по
входу р0 додається одиниця.
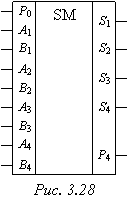
Приклад 18. Розглянути мікросхему К1533ІМ3. Пояснити, як використовувати вказаний чотирирозрядний суматор для додавання: а) двох чотирирозрядних чисел; б) двох дворозрядних та двох однорозрядних чисел; в) двох восьмирозрядних (байтових) чисел.
Розв’язання. При додаванні двох чотирирозрядних слів необхідно вхід переносу Р0 заземлити (рис. 3.28). В дворозрядному суматорі входами є А1, А2 та В1, В2, а виходами S1, S2, S3. Останній є виходом переносу. В однорозрядному суматорі використовуються входи А4, В4, а виходами є S4 та Р4 . При додаванні двох однобайтових слів необхідно наростити два однотипних суматори. При цьому вихід Р4 суматора напівбайтів молодших розрядів з’єднується з входом Р0 суматора напівбайтів старших розрядів слів, що складаються.
Операції знаходження суми та різниці можна поєднати в одному пристрої, як показано на рис. 3.27. Для виконання операції додавання на вхід рі-1 переносу подається сигнал низького рівня. Відповідно на входах елементів ВИКЛЮЧАЮЧЕ АБО число b3 b2 b1 b0 буде представлене в прямому коді. При подачі на вхід рі-1 сигналу високого рівня, як відмічалось раніше, число b3 b2 b1 b0 буде представлене у доповнюючому коді.
Слід нагадати, що при виконанні операції віднімання результат на виході суматора залежить від співвідношення між числами, що беруть участь в операції. При
a3 a2 a1 a0 > b3 b2 b1 b0
результат одержується в прямому коді, а в розряді переносу рі-1 з’являється 1. Коли ж
a3 a2 a1 a0 < b3 b2 b1 b0 ,
тоді результат отримується в зворотньому коді, а в розряді переносу рі-1 одержується 0.
Приклад 19. Розробити пристрій двійкового множення на суматорах та логічних елементах І, що дозволяє множити чотирирозрядне число А на трирозрядне число В.
Розв’язання. Після множення трирозрядного й чотирирозрядного кодів отримується семирозрядний код. Результат операції утворюється за рахунок паралельного множення множеного на кожен розряд множника і складання проміжних добутків зі зсувом на один розряд. При підрахуванні добутку виконуються наступні дії
|
´ |
A4 |
A3 |
A2 |
A1 |
||||||
|
B3 |
B2 |
B1 |
||||||||
|
A4B1 |
A3B1 |
A2B1 |
A1B1 |
|||||||
|
A4B2 |
A3B2 |
A2B2 |
A1B2 |
|||||||
|
A4B3 |
A3B3 |
A2B3 |
A1B3 |
|||||||
|
M7M6 |
M5 |
M4 |
M3 |
M2 |
M1 |
Тут M1 = A1B1, M2 = A1B2 + A2B1, M3 = A1B3 + A2B2 + A3B1, M4 = A2B3 + A3B2 + A4B1, M5 = A3B3 + A4B2, M6 = A4B3, M7 – біт переносу із попереднього розряду. Тут знак “+” – знак арифметичного додавання.
Однорозрядне множення забезпечується елементами I. Суми можуть бути реалізовані суматорами К1533ІМ3.
Для реалізації цієї операції на рис. 3.29 приведена принципова схема.
Приклад 20. Розробити принципову схему суматора, який здійснює додавання однорозрядних десяткових чисел.
Розв’язання. Для додавання десяткових чисел необхідно використати їх двійково-десяткову форму представлення. Це дозволяє для виконання операції додавання використати чотирьохрозрядний суматор двох чисел, наприклад, мікросхему К1533ІМ3.
Відомо [4], що в випадку, коли в результаті додавання отримується результат S > 9, значення молодшого напівбайта є невірним. Для отримання вірного результату необхідно його відкоригувати. Корегування виконуємо шляхом додавання до результату числа 610=01102.
Цю операцію в системі двійково-десяткового числення можна сформувати наступним чином. При появі в результаті додавання двійкових кодів 10102=1010, 10112=1110, 11002=1210, 11012=1310, 11102=1410, 11112=1510 до отриманого результату необхідно додати число 610. Якщо ці коди не з’являються, то додавання числа 610 не робити.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.