Пристрої комбінаційної схемотехніки (Використання базових логічних елементів. Мультиплексори. Арифметичні пристрої. Схеми контролю), страница 11

При контролі парності задається v = 0. Якщо відбудеться контроль за непарною кількістю одиниць, то задається v = 1.

Вихід Y називається контрольним бітом. При прийомі інформації одержане слово знов перевіряється на парність або непарність. Якщо при контролі парності в приймальному контрольному пристрої з’явилась 1, то це значить, що або в інформаційній шині, або в контрольному біті з’явилась похибка. Як бачимо, такий простий контроль не дає можливості виправити похибку, але він дає можливість визначитись з хибною інформацією, щоб потім або використати її, або відкоригувати.

В практиці контролю переважно використовують спосіб контролю по непарності. Пов’язано це з тим, що при появі слова з усіма нулями при контролі по парності цю ситуацію неможливо відрізнити від обриву лінії зв’язку.

Приведена схема не може визначити подвійної похибки і будь-якої кількості парних похибок. Пояснюється це лише малою надмірністю лінії зв’язку. Тому для більш глибокого контролю необхідно мати і більшу її надмірність. Оскільки цифрові лінії зв’язку дуже надійні і ймовірність появи двох незалежних похибок р₂ = р₁², тому навіть такий простий контроль суттєво піднімає надійність передачі інформації. Завдяки цьому цей вид контролю використовується практично в усіх каналах передачі цифрових даних, а також при роботі процесора з запам’ятовуючими пристроями, контролюючи тим самим і пристрої пам’яті.

Пристрої контролю парності/непарності двійкових слів випускаються у вигляді самостійних мікросхем у різних серіях (КМОН – 561СА1, ТТЛ – К1533ІП2, 531ІП5).

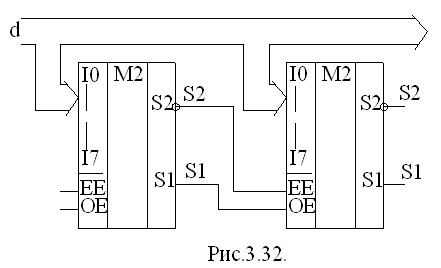
Мікросхема К1533ІП2 (рис. 3.32) (зарубіжними аналогами якої є мікросхеми 74180PC, CDB4180E, SN74180N, UCY74180N) має вісім інформаційних входів І0 – І7 та два входи ОЕ та ЕЕ, які дозволяють в одній схемі забезпечити різні режими роботи: керування полярністю вихідних сигналів, нарощування розрядності схем контролю, забезпечення контролю як по парності, так і по непарності одиниць.

Табл. 3.11
Число одиниць на І0 – І7	EE	OE	S1	S2
Парне	1	0	1	0
Непарне	1	0	0	1
Парне	0	1	0	1
Непарне	0	1	1	0
Х	1	1	0	0
Х	0	0	1	1

Виходи S1, S2 взаємно інверсні. Вихід S1 є виходом непарності. Взаємозв’язок між значеннями вхідних та вихідних сигналів приводиться в Табл. 3.11. Таблиця дає можливість визначитись з необхідними вхідними сигналами на входах ЕЕ і ОЕ для забезпечення контролю по парності або непарності. Наприклад, при вхідних сигналах ЕЕ = 1; ОЕ = 0 парність коду на входах І0 ÷ І7 буде відображатись високим рівнем виході S1 та низьким на S2. Якщо ж на входах І0 ÷ І7 код непарний, то на виходах S1, S2  буде код, інверсний попередньому.

Слід звернути увагу на те, що при парності коду на входах І0 ÷ І7 маємо наступні логічні співвідношення між вхідними і вихідними сигналами:

при непарності коду:

Нарощування довжини слова що підлягає контролю забезпечується послідовним з’єднанням мікросхем, причому виходи S1 та S2 попередньої схеми з’єднані з входами ЕЕ та ОЕ наступної.

Корекція похибок. Розглянутий спосіб оцінки достовірності передачі інформації по каналу зв’язку не дає можливості знайти похибку в інформаційному слові. Тому в складних комп’ютеризованих та мікропроцесорних схемах з розгалуженими каналами цифрового зв’язку використовують системи передачі з використанням таких кодів, які дозволяють як знаходити, так і виправляти випадкові похибки. До них відносяться, наприклад, код Хемінга, циклічні коди, які використовуються для виявлення та виправлення похибок не тільки при передачі, але й при зберіганні даних, код Ріда-Соломона, який широко використовується при записі та зчитуванні компакт-дисків та інші. Розглянемо ідеологію та принцип побудови цифрових кодерів з виправленням похибок  на прикладі використання коду Хемінга.

Припустимо, що необхідно визначити та виправити одиничну похибку двійкового коду з n інформаційними розрядами. До цього коду додається m контрольних кодів. В результаті одержуємо кількість символів в коді

.

(3.13)

При передачі кодів може бути спотвореним будь-який інформаційний сигнал. Але може виникнути й така ситуація, коли жоден з розрядів не буде спотворений, тобто, якщо в створеному коді маємо N розрядів, то за допомогою контрольних кодів, що входять, відповідно до (3.13) в це число, повинна бути створена така кількість комбінацій 2^m, щоб мати можливість закодувати будь-який з розрядів.

Тому повинна виконуватись нерівність:

(3.14)

або відповідно до (3.13)

.

(3.15)

З (3.14) з врахуванням (3.15) знаходимо:

.

(3.16)

З (3.16) знаходиться кількість інформаційних розрядів в кодованому слові з N розрядами:

.

(3.17)

Критерій оптимальності коду Хемінга має вигляд:

,

(3.18)

де С_N ^r – кількість комбінацій з N по r ; r – кількість виявлених незалежних похибок.

При r = 1 (тобто для одиничних похибок) формула (3.18) має вигляд:

.

(3.19)

Формула (3.19) є нижньою межею коду, так  як встановлює те мінімальне співвідношення коригуючих та інформаційних розрядів, нижче якого код не може зберігати свої коригуючі здібності.

Як приклад, розглянемо ситуацію, коли слово має 11 розрядів (n = 11). В цьому випадку формула (3.17) перетворюється в рівність при N = 15. Тобто кількість коригуючих розрядів m = 4.

Пояснимо, що можливість виправлення похибки в коді Хемінга базується на повтореній k разів системі контролю парності, але не всього слова одночасно, а k окремих груп його розрядів. Слово розбивається на групи так, щоб номер кожного розряду визначався за його належністю до цих груп. Вказані групи називаються групами контролю парності і компонуються з розрядів кодового слова на основі наступних правил: