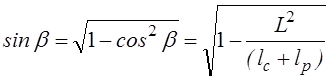Определение сил взаимодействия машины с деревом при валке и перемещении деревьев. Определение сил сопротивления перемещению дерева и параметров приводов рычагов захватных устройств, страница 6

.                       (3.3)

Подставляя выражение (3.3) в уравнение (3.1), получаем

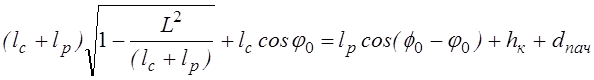          (3.4)

Итак, имеем систему алгебраических уравнений:

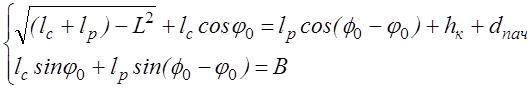                    (3.5)

содержащую два основных проектных параметра l_c, l_p, а также два параметра φ₀, ψ₀, определяющих компоновку стрелы и рукояти. Третий параметр, характеризующий компоновку манипулятора на машине, - высота колонны h₀ - в уравнение связей (3.5) не входит.

Решим систему уравнений (3.5) относительно основных проектных параметров l_c, l_р.

Рассмотрим частные случаи компоновки манипуляторов в положении рабочего органа над коником, характеризующимся углами φ₀, ψ₀.

В случае, когда углы равны, т.е. φ₀ = ψ₀ справедливо равенство , и уравнение длин принимает вид:

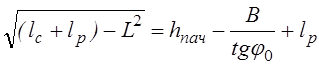.                         (3.6)

Для решения этого уравнения освободимся от радикала:

.

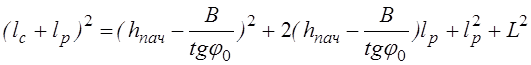После преобразований находим:

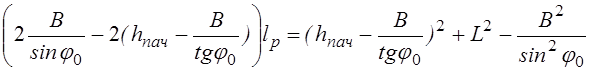, откуда имеем расчетную формулу для определения длины рукояти

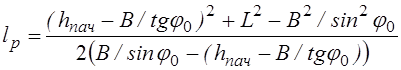.                               (3.7)

Используя равенство , получаем искомое выражение для суммы длин:

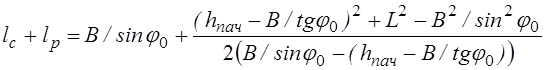.                (3.8)

Во втором случае, когда угол ψ₀ = 2φ₀, имеем:

, и уравнение длин принимает вид:

.

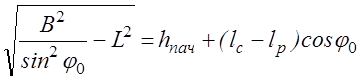Произведя преобразования, получаем систему

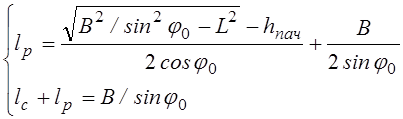.                     (3.9)

В третьем случае, когда ψ₀= 0, имеем

, и уравнение длин

.

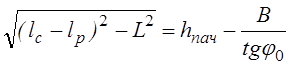Освободившись от радикала, запишем систему алгебраических уравнений

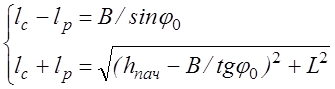.                                (3.10)

Полученные аналитические зависимости [7] между проектными параметрами манипулятора не учитывают ограничения на положение шарнира сочленения стрелы манипулятора с поворотной колонной, оцениваемого величиной h₀. Технически манипулятор можно установить непосредственно на платформе (без поворотной колонны), но при этом формируемая пачка будет ограничивать перемещение рабочего органа над коником, а также перемещение из положения над коником к предмету труда, находящемуся на земле. Высота поворотной колонны должна быть такой, чтобы формируемая в конике пачка не приводила к функциональным ограничениям манипулятора. Если же по техническим условиям предусмотрен его поворот относительно оси колонны на угол 360°, то в данном случае высота кабины не должна создавать функциональных ограничений на перемещение манипулятора.

Обозначим H_к высоту кабины над технологической платформой. Тогда условие отсутствия функциональных ограничений манипулятора можно записать в виде:

, т.е. допустимая высота точки подвеса манипулятора к машине должна быть больше или, по крайней мере, равна максимальной из величин d_пач , H_к .

Установим связь между проектными параметрами манипулятора и высотой шарнира сочленения стрелы с поворотной колонной. Уравнение длин в проекции на ось колонны в соответствий с рисунком 3.1 можно записать в следующем виде:

.

Проектные параметры манипулятора  l_с, l_р, φ₀, ψ₀ должны удовлетворять условиям:

,

При φ₀ = ψ₀ имеем

.                      (3.11)

При ψ₀ = 2φ₀ и ψ₀ = 0

                                      .                  (3.12)

Присовокупив равенство (3.11) к формулам (3.7), (3.8), а равенство (3.12) к формулам (3.9), (3.10), получим систему уравнений, определяющих проектные параметры манипулятора l_с, l_р, φ₀, причем эта совокупность параметров в каждом частном случае удовлетворяет условию минимальной суммарной длины l_с + l_р. В этом легко убедиться, обратившись к кинематической схеме манипулятора, представленной на рисунке 3.2, из которой следует равенство  . Минимальная суммарная длина достигается при наименьшем значении величины h₀.

Пример расчета проектных параметров манипулятора для трех случаев компоновки. Исходные данные: максимальный вылет L= 6 м, высота технологической платформы h_к= 1,75 м, объем пачки V_пач = 8,5 м³, средний диаметр деревьев D_ср = 36 см, высота рабочего органа h_з = 1,2 м, расстояние коника от оси поворотной колонны В = 1 м,

Среднему диаметру D_ср = 36 см соответствует объем ствола V_хл = 1,2 м³ (рисунок 3.2 [7]).

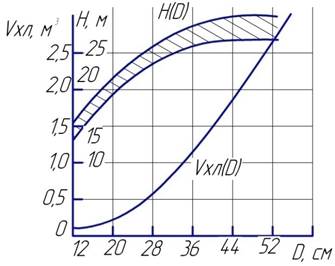
Рисунок 3.2 – Зависимость объема ствола и диапазона высот от диаметра на высоте груди

Число деревьев в пачке

,

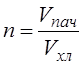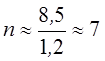
При n = 7 по данным для определения относительного диаметра пачки имеем, откуда получаем: