Определение сил взаимодействия машины с деревом при валке и перемещении деревьев. Определение сил сопротивления перемещению дерева и параметров приводов рычагов захватных устройств, страница 2

Пусть стрела поворачивается вокруг шарнира О с угловой скоростью , а рукоять поворачивается вокруг точки О₁ с той же скоростью, но в обратном направлении. Тогда получим пару вращения, и любая точка рукояти будет двигаться поступательно с максимальной скоростью стрелы:

,                                                      (1.1)

где l₁ – длина стрелы,

 - угловая скорость вращения стрелы.

В данном случае точка М будет двигаться по некоторой кривой малой кривизны и с высокой степенью точности ускорение точки М можно считать равным нулю. Тогда уравнение вращения дерева будет иметь вид такой же, что и при вращении относительно неподвижной оси:

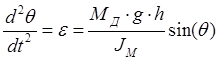;                                         (1.2)

где М_Д – масса дерева,

g – ускорение свободного падения,

h – расстояние от торца комля до центра тяжести дерева.

J_M – момент инерции дерева относительно точки М.

Θ – угол между продольной осью дерева и вертикалью при падении .

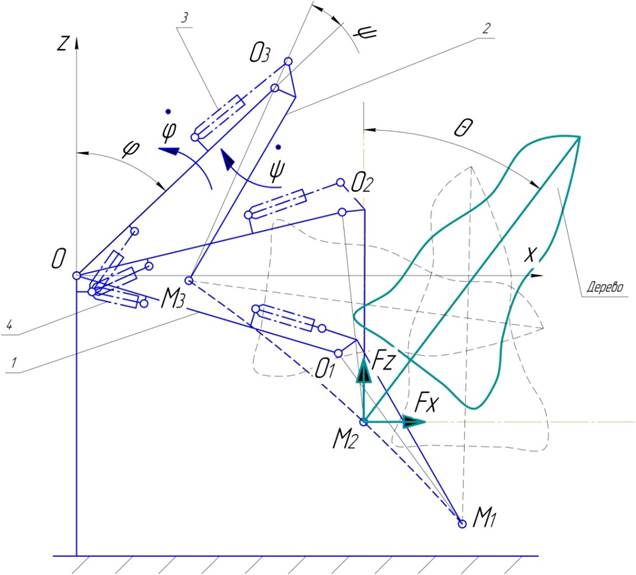
Рисунок 1.1 – Схема взаимодействия манипулятора с деревом

1 – стрела, 2 – рукоять, 3 – гидроцилиндр поворота рукояти,

4 – гидроцилиндр подъёма стрелы

После интегрирования уравнения вращения дерева получим выражение для угловой скорости вращения дерева при падении:

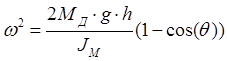;                                        (1.3)

2 Определение массовых характеристик дерева.

Массу дерева можно достаточно точно определить по следующим эмпирическим формулам [5], где d – диаметр дерева на высоте груди в см. :

- для сосны ,

- для ели ,

- для осины ,

- для березы в зимний период ,

»»      в летний период .

Положение центра тяжести дерева можно определить на основе многочисленных теоретических и экспериментальных исследований, в результате которых установлено, что центр тяжести дерева располагается на высоте (0,36 – 0,40)Н, где Н – высота дерева. [3,4]. Таким образом:

.                                                    (1.4)

Момент инерции дерева относительно комля – J_о определяется по формуле [2]:

J_о = 0,21 mh²_д;                                            (1.5)

3 Построение траектории движения точки М – рисунок 1.1.

По условию поступательного равномерного движения рукояти имеем:

,                                        (1.7)

,

Траектория представляется следующим уравнением:

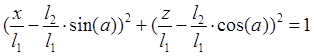.                                   (1.8)

где l₂ – длина рукояти.

В начальный момент времени имеем:

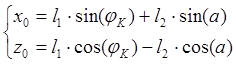;                                      (1.9)

Решая уравнения относительно неизвестных а и , находим угловые величины в момент срезания дерева  и . - начальный угол между стрелой и рукоятью, а  - начальный угол между стрелой и осью Z в момент срезания дерева.

В качестве начальных условий принимаются координаты Х0, Z0 расположения захватно - срезающего устройства в момент среза дерева точка М. (Приведены в исходных данных). Решение системы уравнений производим в программе MathCAD в соответствии с приведённым ниже примером решения такой системы, где х и у равные 0 необходимы в качестве начальных условий для алгоритма решения подобных уравнений, а х и у входящие в уравнение являются искомыми значениями соответственно углов  и  в радианах:

Пример решения системы уравнений в программе MathCAD:

X₀ = 6 м, Z₀ = 3 м. Начальные условия по исходным данным.

Команда, запускающая решение.

Начальные условия для алгоритма решения.

Решаемая система

Функция поиска решения.

Здесь х это = 0,531 рад, а у – а = 1,458 рад

После нахождения искомых величин необходимо построить траекторию движения точки М произвольно задаваясь временем t = 0; 1; 2; 3; и т.д. до 10 секунд по следующим зависимостям:

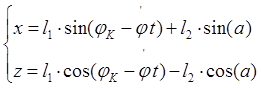;                                  (1.10)

Построение траектории произвести в координатах z и x. Далее на траектории необходимо отметить время, которому принадлежит каждая построенная точка. Зная время вычислить угол Θ на основании зависимости его от времени, имеющей следующий вид:

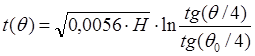;                                   (1.11)

где Н – высота срезаемого дерева,