находят по ним из прил.2 значения интеграла вероятности и затем вычисляют вероятность.
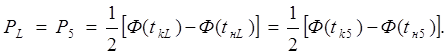
Таким образом вычисляют вероятность PLпопадания случайной величиной X в каждый интервал L(см. гр.4 таблицы). Затем вычислят другие величины, необходимые для расчета значения æ2q (гр10-13 таблицы). В нашем примере æ2q = 7,72.
Поскольку число степеней свобода r=k-c-1 (где общее число интервалов k= 7), а число параметров Сопределяемых на основании наблюдаемых данных, равно двум (параметры x-и 6 ), подучим r=7-2-1=4,
По прил.1 (r=4 и æ2q=7,72) определяют вероятность P(æ2≥ æ2q) того, что значение æ2 превзойдет значение æ2q Получим P(æ2≥ æ2q )=0,104.
Значение P(æ2≥ æ2q) достаточно велико по сравнению с уровнем Pq =0,05, и,следовательно, можно считать, чти гипотеза о согласии наблюдаемых данных с законом нормального распределения на опровергается.
Порядок выполнения работы
.
1. Получить у преподавателя вариант экспериментальной выборки, подлежащей проверке на нормальность распределения..
2.. По формуле (3) вычислить число интервалов группирования, производя округление до целого числа.
3. По формуле (4) вычислить значение постоянного интервала
4. Записал значения вычисленных интервалов в гр. 2 расчетной таблицы вычерченной по аналогии с приведенной в данной работе.
5. Подсчитать изаписать в гр. З таблицы число элементов выборки, попавших в каждый интервал Д=1,2,……,k.
6. По формуле (8) вычислить значения x-и 6.
7. Заполнить вое графы таблицы, произведя необходимые вычисления в соответствии о изложенным в описании порядком и приведенной таблицей.
8. По вычисленному значению æ2q и r найти вероятность P(æ2≥ æ2q) и сделать вывод о согласии (и несогласии) наблюдаемых данных с законом нормального распределения.
9. По экспериментальным данным (гр. З и 10 таблицы) построить гистограмму (см. рисунок, кривая 1) и по формуле (1) -кривую нормального распределения, сглаживающую эту гистограмму (кривая 3 ).
10. Оформить отчет и защитить его у преподавателя.
Работа 3. ОПРЕДЕЛЕНИЕ ИНТЕРВАЛА ОПРОБОВАНИЯ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ ОБОГАЩЕНИЯ ПРИ ДИСКРЕТНОМ
КОНТРОЛЕ.
Цель работы
Для одного из интервалов экспериментальной выборки (плотности или гранулометрического состава слава мельницы) определить интервал опробования при дискретной контроле.
Общие сведения
Вопрос выбора интервала опробовании стоит перед исследователем, приступающим к изучению какого-либо объекта с целью как отработки технологического режима, так к его автоматизации. Начальным этапом исследования, как. правило, является серия дискретных ручных измерений ряда величин, характеризующих работу объекта, с последующим расчетом требуемых характеристик.
Завышенная частота измерений ведет к усложнению конструкции систем автоматического контроля, а при ручном замере - к увеличению затрат труда на взятие проб и их анализ. Заниженная частота измерений практически может свести к нулю результаты дискретного контроля, поскольку при этом невозможно проследить с необходимой точностью за изменением значений контролируемой величины.
Расчетные формулы для определения частот измерений при дискретном контроле можно получить, если известна сценка корреляционной функции и анализируемые величины имеют предварительный дискретный контроль. Однако, как правило, предварительный дискретный контроль не выполняется, т.е. оценки корреляционных функций анализируемых величин неизвестны. В таких случаях предварительные оценки частоты замеров получают в результате пробных опытов. Имеется следующая методика оценки интервалов между соседними измерениями, разработанная Э.Л.Ицковичем.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.