Одно из главных условий применимости выборочного метода к опробованию полезных ископаемых» помимо требования случайного характера изменчивости контролируемого компонента и статистической достаточности числа частичных проб, состоит в том, что распределение контролируемых компонентов в добытых полезных ископаемых и продуктах обогащения должно подчиняться закону нормального распределения или. мало отличаться от него.
Появление какого-либо значения xiконтролируемого компонента как результата обработки и анализа пробы является случайным событием. Существует некоторая вероятность появления этого значения в интервале dxi, определяемая как xi/dxi.
Случайная величина Xподчиняется закону нормального распределения» если ее плотность вероятности f(xi), или частость с которой появляются отдельные значения вариационного ряда, может быть представлена в виде:
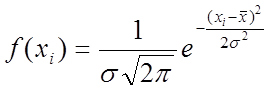 |
Коэффициент перед экспонентой подобран таким образом» что интеграл от f(xi), взятый от -оо до +оо, был равен единице. Результата анализа всегда дискретны, поэтому на практике обычно задается конечное значение интервала dxi. В этом случае относительные частота попадания xiв заданный интервал изображаются в виде гистограмм и полигонов распределения. Если
|
|
|
Экспериментальное (1) и теоретические (2,3) распределения |
на ось абсцисс нанести в масштабе границы интервалов, а на ось ординат - частоту наблюдений в каждом интервале, то получим ступенчатую диаграмму - гистограмму (см. рисунок, кривая 1), Если середины всех верхних оснований прямоугольников частот соединить ломаной линией, то получим полигон частот (кривая 2). Число относительных частот, приходящихся на единицу ширины интервала, называют плотностью распре-деления.
Таким образом, в эмпирическом распределении плотность вероятности заменяется плотностью частости (частость на единицу интервала).
Одна из задач статистической обработки материала заключается в подборе для данного статистического ряда такой теоретической плавной кривой распределения, которая бы, с одной стороны, достаточно хорошо описывала наблюдаемые значения случайной величины, а с другой - была бы удобна для дальнейшего статистического анализа. Такая задача называется задачей выравнивания: (сглаживания) статистических рядов.
Очень часто при исследовании какой-либо случайной величины исходят из предположения, что последняя подчиняется закону нормального распределения, и задача выравнивания переходит в задачу о рациональном выборе параметров xiи 6 в выражении (I).
Вместе с тем, как бы хорошо ни была подобрана теоретическая кривая, между ней и эмпирическим распределением неизбежны некоторые расхождения. Поэтому возникает вопрос, объясняются ли эти расхождения только случайными обстоятельствами, связанными с ограниченным числом наблюдений, или они являются существенными и связаны с тем, что подобранная кривая плохо выравнивает данное статистическое распределение.
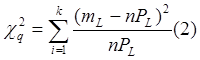 |
где k- число интервалов (разрядов); mL - число элементов выборки, попадающих в каждый интервал L; n- общее число попаданий элементов статистического ряда в разряда, вычисленные по принятому теоретическому закону распределения.
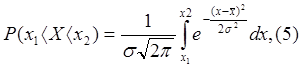 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.