и считать, что гипотеза не опровергается; если она мала, то делается вывод о том, что гипотеза не согласуется с опытным распределением. Обычно принимается Pq= 0,03+0,05.
Проверяя согласованность теоретического и эмпирического распределения, исходят из расхождения между теоретическими npLи наблюдаемыми тLчастотами. Чтобы найти число попадания исследуемой переменной в интервал Lпри объеме выборки n > 40, выборочные данные группируют следующим образом. Находят минимальные и максимальные значения признака в выборке и полученный диапазон xmax-xmin разбивают на определенное число интервалов группирования
![]()
тогда постоянный интервал
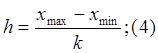
Затем определяют начальные и конечные значения интервалов в порядке возрастания (см, таблицу). Далее подсчитывают число выборочных данных, попавших в каждый интервал (гр.3 таблицы).
Для определения теоретического числа прLпопадания случайной величины X в интервал Lнеобходимо (на основании принятого закона нормального распределения) вычислить теоретические вероятности. На основании формулы (I) вероятность попадания случайной величины X в интервал (x1,x2) равна интегралу:
С помощью замены (x-x-)/6=U,dx/6=dU этот интеграл приводят к виду
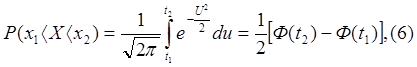
Вычисление критериев согласия Пирсона
|
№ п/п |
Значение интервала XL |
mL |
PL |
tнL |
tkL |
Ф(tнL) |
Ф(tkL) |
ФL |
NPL |
mLnPL |
(mL-nPL)2 |
* |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
1 |
56,8-58,37 |
6 |
0,130 |
-2,016 |
-1,31 |
0,9566 |
0,8080 |
-0,0743 |
3,42 |
2,58 |
6,65 |
1,94 |
|
2 |
58,37-59,94 |
5 |
0,108 |
-1,323 |
-0,685 |
0,8080 |
0,4908 |
-0,1586 |
7,29 |
-2,29 |
5,24 |
0,719 |
|
3 |
59,94-61,51 |
13 |
0,282 |
-0,664 |
-0,059 |
0,4908 |
0,0478 |
-0,2215 |
10,18 |
2,28 |
7,95 |
0,78 |
|
4 |
61,51-63,08 |
9 |
0,195 |
-0,0597 |
-0,565 |
0,0478 |
0,04245 |
0,18835 |
8,66 |
0,34 |
0,11 |
0,0133 |
|
5 |
63,08-64,65 |
8 |
0,177 |
-0,565 |
1,16 |
0,4245 |
0,7540 |
0,16475 |
0,23 |
0,18 |
0,18 |
0,2444 |
|
6 |
64,65-66,22 |
0 |
0 |
1,16 |
1,42 |
0,7540 |
0,8444 |
0,0452 |
2,08 |
4,32 |
4,32 |
2,079 |
|
7 |
66,22-67,79 |
5 |
0,108 |
1,42 |
2,043 |
0,8444 |
0,9586 |
0,0571 |
2,38 |
2,62 |
6,56 |
2,16 |
|
Χ2g=7,7157 |
||||||||||||
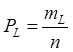
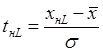
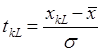
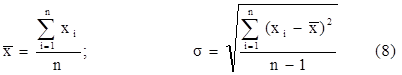 |
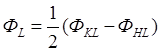
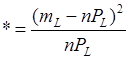
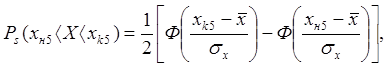 |
где
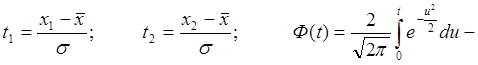 интеграл вероятности (функция Лапласа).
интеграл вероятности (функция Лапласа).
Для положительных значений tсоставлены таблицы (прил.2). Значения Ф(t) при отрицательных значениях tвычисляют с помощью свойства нечетности этой функции:
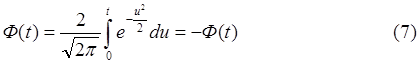
Кроме конкретных значений начала и конца интервала, необ-ходимо знать также численные значения параметров x и 6 рассматриваемой выборки:
Тогда вероятность попадания случайной величины X, например, в пятый интервал где xн5 и xк5- численное значение соответственно начала и конца пятого интервала.
Вычисляя значения величин
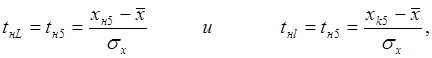
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.