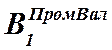Резьбовые соединения: Методическое пособие по самостоятельному выполнению студентами расчетно-графических работ, страница 20

 и 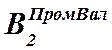 - ширина опорных подшипников на промвалу со  стороны шестерни и зубчатого колеса соответственно,

- углубления обоих подшипников в стенку корпуса редуктора (со стороны шестерни и колеса),

 - зазоры между стенкой редуктора и вращающимися боковыми сторонами шестерни и колеса,

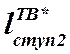 - ширина ступицы колеса тихоходного вала,*она включена в расчётную длину промвала, так как  ширина ступицы колеса тихоходного вала больше чем ширина сопряжённой с колесом ширины  шестерни (зубчатая прямозубая пара №3),

(смотри расчёт п.8,4:   ).

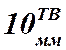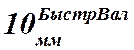 и  - ширина втулки на тихоходном и быстроходном валах, соответственно, между подшипниками этих валов и зубчатыми колёсом и шестернёй,

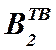 и 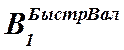 - ширина подшипников тихоходного и быстроходного валов в центральной части редуктора (в месте торцевого стыка этих валов),

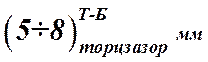 - торцевой зазор между соосными тихоходным и быстроходным валами,

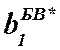 - ширина зубчатого венца косозубой шестерни быстроходного вала, *она включена в расчётную длину промвала, так как ширина этой шестерни больше ширины ступицы сопряжённого с ней косозубого колеса промвала этой зубчатой пары (зубчатая косозубая быстроходная пара №4), (смотри расчёт п.8,4:  ).

            Определим расчётную длину промежуточного вала по его габаритной длине:

 ,

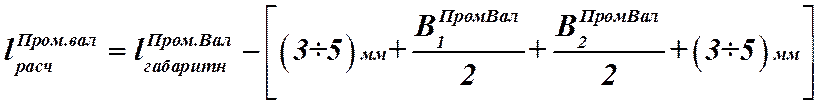Определим  - отрезок А2 диаграммы - расстояние между зубчатым колесом промвала (косозубая зубчатая пара №4) и подшипником промвала со стороны этого колеса:

                        ,

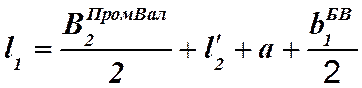Определим  - отрезок Б1 диаграммы – расстояние между шестернёй промвала (прямозубая зубчатая пара №3) и подшипником промвала со стороны этой шестерни:

                        ,

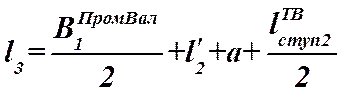Определим  - отрезок 1-2 диаграммы – расстояние между осями шестерни и колеса промвала:

                        .

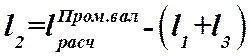мм,  мм,   мм. 

Примечание:  Получение этих трёх длин (l₁l₂l₃) графическим или расчётным путём определяется студентом самостоятельно.

Из пунктов  7.1  и   7.2 настоящего расчета берём значения  усилий на зубьях колеса и шестерни:

- для колеса:

окружная сила 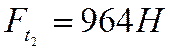, радиальная сила 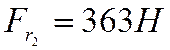, осевая сила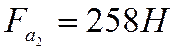  

- для шестерни:

окружная сила 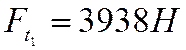, радиальная сила 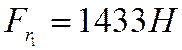, осевая сила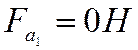

Причем осевая сила на прямозубой шестерне не создается, а  осевая сила на косозубом колесе промежуточного вала парируется равномерно двумя опорами промежуточного вала, радиальными шарикоподшипниками, т.е. 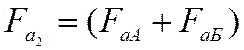 .   Тогда

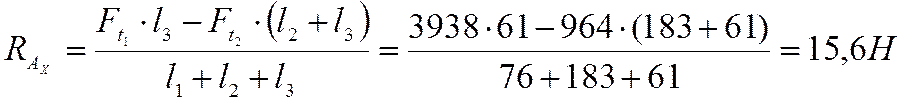
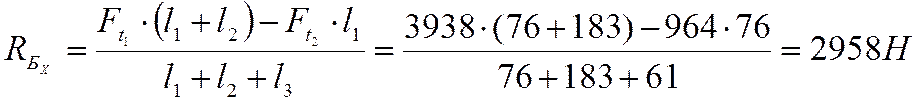
Находим изгибающие моменты в вертикальной плоскости XOZ.

Момент в сечении колеса (2):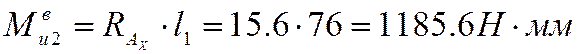  

Момент в сечении шестерни (1):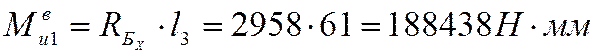

9.1.2 Изгиб в горизонтальной плоскости YOZ. Определение реакций опор 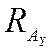   и

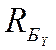
Все силы, приложенные к промежуточному валу, находятся в равновесии.  Найдем суммы изгибающих моментов в плоскости YOZ :

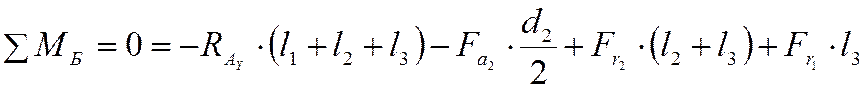
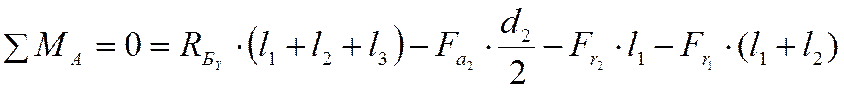
тогда: ,    и

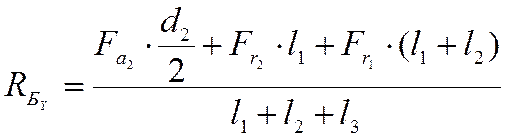            .    Окончательно:

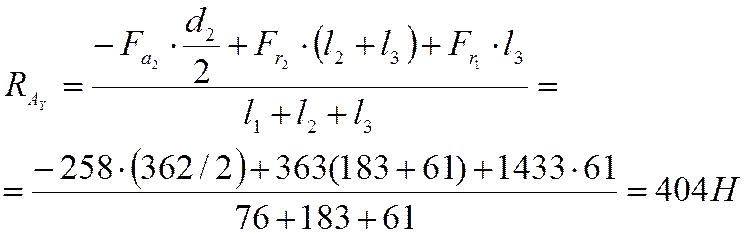
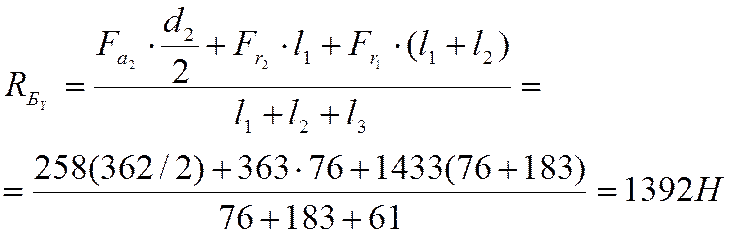
Находим изгибающие моменты в горизонтальной плоскости YOZ.

Момент в сечении колеса (2):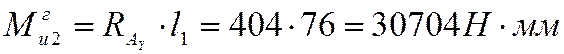  

Момент в сечении колеса (2) с учетом :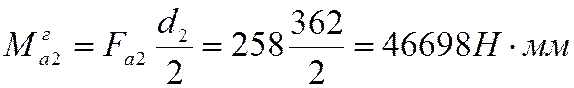

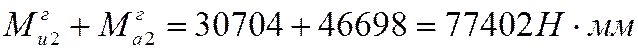
Момент в сечении шестерни (1):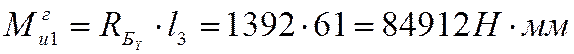

9.1.3 Находим суммарные радиальные реакции опор промежуточного вала

Найдем геометрическую сумму реакций опор в точках А и Б:

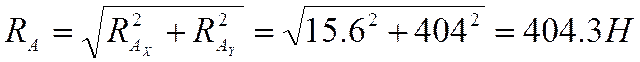
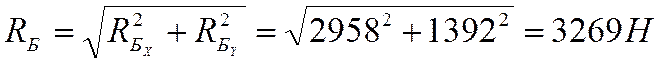
9.1.4 Находим изгибающие моменты в сечениях вала, соответствующих местам расположения колеса и шестерни

- изгибающий момент в сечении вала, где расположено колесо.  Это сечение на расстоянии от опоры А - :

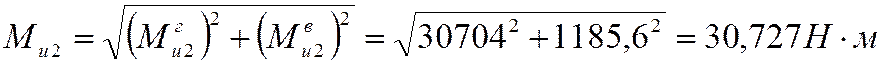
- изгибающий момент в сечении вала, где расположена шестерня.  Это сечение на расстоянии от опоры Б - :

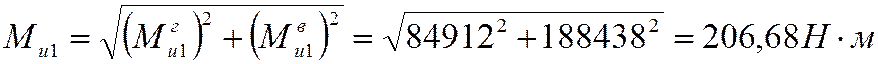
9.1.5 Определение крутящего момента

Согласно  п. 7.2.6 крутящий момент на промежуточном валу создается окружными усилиями на колесе 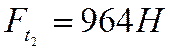 и шестерне 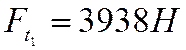. Крутящий момент на промежуточном валу равен   .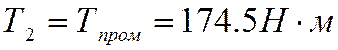

            Диаметр вала в сечениях колеса и шестерни одинаков и равен . Крутящий момент одинаков в обоих сечениях. Изгибающий момент существенно больше в сечении вала, где расположена шестерня и равен .

            Поэтому проверку прочности вала будем производить в сечении шестерни.

Для изготовления  промежуточного вала мы приняли  Сталь 40Х со следующими механическими характеристиками: ,   ,

, , , твердость .

,    ,    .

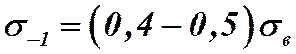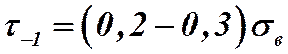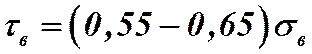9.1.6 Определение приведенного момента сил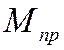

Согласно принятых по курсу «Сопротивление материалов» расчетов приведенный момент сил в критическом сечении вала находится по формуле:

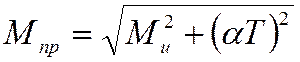, где крутящий момент  , 

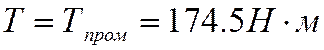изгибающий момент ,  коэффициент ,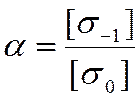

где  - допускаемое знакопеременное напряжение для материала вала,

и     - допускаемое пульсирующее напряжение для материала вала.

Найдем коэффициент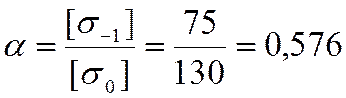 

Определим  приведенный момент для опасных сечений:

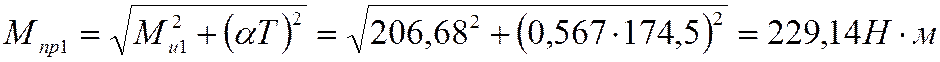
Так как  , то считаем критическим сечение вала в районе шестерни (1).  Определим расчетный диаметр промежуточного вала в критическом сечении:

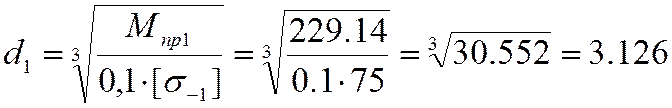мм, что значительно меньше принятого диаметра 50мм.

9.2 Проверка статической прочности вала

Расчёт статической прочности выполняется как проверочный.

(ВТ Павлище учебник  «Основы конструирования и расчета деталей машин», стр. 426)

1. Находим номинальное напряжение в критическом сечении (1).

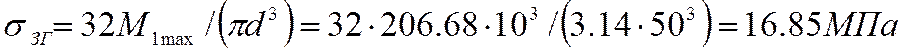
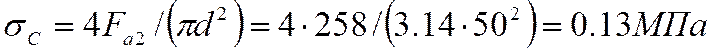
2, Находим эквивалентное напряжение.

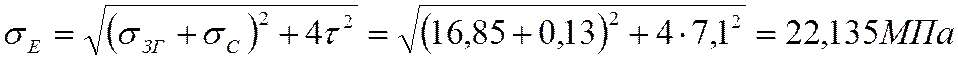
3. Находим максимальное эквивалентное напряжение при кратковременных перегрузках

4. Допустимое эквивалентное напряжение

Условия статической прочности вала удовлетворяются,  поскольку:

9.3 Расчет на сопротивление усталости промежуточного вала

            Этот расчет валов выполняется как основной на усталостную прочность при длительных циклах эксплуатации. Он заключается в определении расчетных коэффициентов запаса прочности в предположительно опасных сечениях. В нашем случае это сечение, где расположена прямозубая шестерня 1 (в этом месте диаметр промвала d₃=d₁=50мм).

            Для критического сечения 1 определяем коэффициент запаса прочности  и сравниваем его с допускаемыми значениями , которые принимаем обычно 1,3-2,1.