Резьбовые соединения: Методическое пособие по самостоятельному выполнению студентами расчетно-графических работ, страница 17

Значение коэффициента формы зуба  для внешнего зацепления.

            Таблица 14

Коэффициент смещения инструмента Х
Z или ZV	- 0.4	- 0.25	- 0.16	0	0.16	0.25	0.4
16				4.28	4.02	3.78	3.54
20			4.40	4.07	3.83	3.64	3.50
25		4.30	4.13	3.90	3.72	3.62	3.47
40	4.02	3.88	3.84	3.70	3.61	3.57	3.48
60	3.78	3.71	3.68	3.62	3.57	3.54	3.50
80	3.7	3.66	3.63	3.61	3.55	3.55	3.51
100	3.66	3.62	3.61	3.61	3.56	3.56	3.55
180	3.62	3.62	3.62	3.62	3.59	3.58	3.56
	3.63	3.63	3.63	3.63	3.63	3.63	3.63

Степень точности передачи определяем по таблице 12 [1] в зависимости от окружной скорости колеса тихоходной пары: , где  сек^-1 угловая скорость тихоходного вала, сопряженного с грузовым барабаном.  мм, делительный диаметр зубчатого колеса, насаженного на тихоходный вал. Тогда окружная скорость колеса 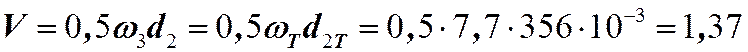м/с. При окружной скорости меньше 2 м/с, согласно таблицы 12, степень точности передачи  9.

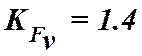 - коэффициент динамической нагрузки определяем согласно стр. 36 [1] (строка для прямозубых колес с твердостью ). см п. 7.1.8  настоящего пособия.

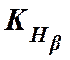 - принимают по табл. 11 п. 7.1.1;

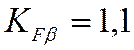- этот коэффициент определяется коэффициентом , расположением опор вала относительно колеса (несимметричное) и твердостью зубьев () . В пункте 7.1.1 б)  настоящего расчета коэффициент ширины колеса относительно межосевого расстояния  равен .

 - коэффициент формы зуба колеса. Определяется  по таблице 14[1] (стр. 57 настоящего расчёта) в зависимости от эквивалентного числа зубьев колеса . для прямозубого колеса . Коэффициент смещения режущего инструмента принимаем . 

Тогда .

 - коэффициент вычисляем по формуле 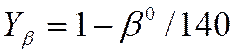 - для косозубых колес. Для прямозубого колеса , поэтому .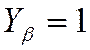

- окружная сила на зубе колеса , (п.7.1.7)

- ширина венца зуба колеса , (п.7.1.6)

- модуль зубчатой пары ,    (п.7.1.2).

Расчетное напряжение изгиба в зубе колеса (на тихоходном грузовом валу) равно

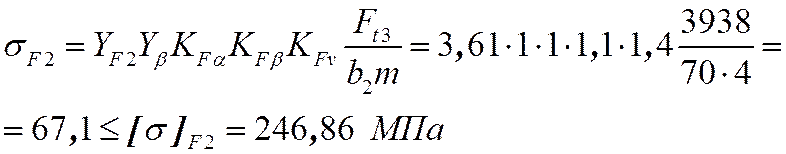
Неравенство соблюдается – значит расчетные напряжения изгиба в пределах допускаемых.

7.2  Расчет быстроходной цилиндрической косозубой  зубчатой пары (пара №4)

В кинематической схеме на рис. 2.18 эта зубчатая пара изображена под № 4.

            Ввиду того, что по заданию редуктор должен быть  с соосными быстроходным и тихоходным валами, то расчет ведем исходя из равенства: мм

7.2.1  Определим предварительно основные размеры колеса, мм:

            Определяем коэффициент ширины колеса относительно межосевого расстояния  . Согласно таблицы в п 7.1.1б) (стр 53 настоящего расчёта) колесо расположено крайне несимметрично. Поэтому, руководствуемся строкой 2 (несимметричное расположение колеса на валу) и крайним значением столбца 2 этой строки (0,25…0,4), получаем

- Тогда ширина зубчатого венца колеса равна: ,

- Модуль зубчатой пары  

Значения модуля округляем до стандартного в большую сторону, предпочтительно из первого ряда таблицы стандартных значений модулей (п. 7.1.2 настоящего расчёта): .

7.2.2  Определим угол наклона и суммарное число зубьев косозубой цилиндрической пары.

- минимальный угол наклона зубьев косозубого цилиндрического колеса: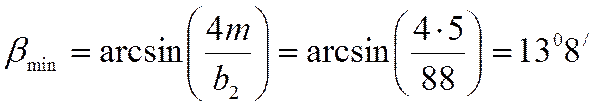

- суммарное число зубьев этой пары: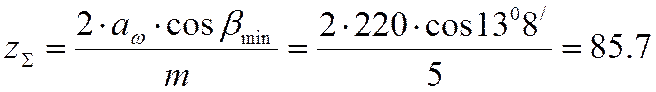

            Полученное значение  округляем до ближайшего меньшего целого числа, т.е. .             Определяем действительное значение угла наклона зуба:

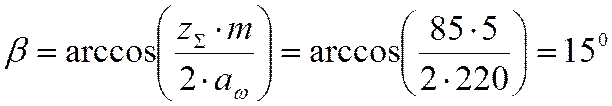
7.2.3 Определяем число зубьев шестерни и колеса косозубой цилиндрической пары (№4).

- определяем число зубьев шестерни 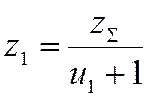, где 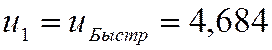 передаточное число косозубой зубчатой пары перехода с быстроходного вала на промежуточный (пара №4 по кинематической схеме рис. 2.18),  суммарное число зубьев пары №4. Тогда:

число зубъев косозубой шестерни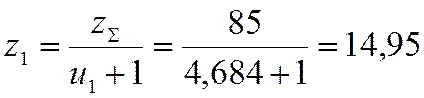  

Чтобы знать в какую сторону мы сможем округлить расчетное число зубьев, определим минимально допустимое значение зубьев для косозубых шестерен:

Отсюда следует, что может быть  или

- определяем число зубьев колеса для обоих случаев:

  или      

7.2.4  Определяем фактическое передаточное число  и его отклонение от расчетного

при этом  должно быть целым и расхождение между номинальным  и полученным передаточным числом  не должно превышать 2,5% при  и 4% пр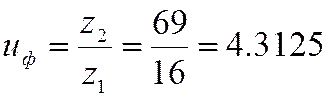и

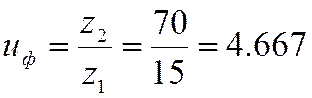  и 

   и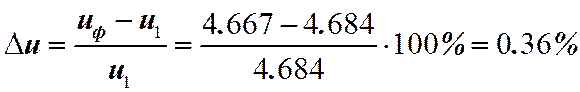   

Из указанных сравнений  мы видим, что при 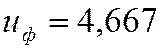отклонение от            не превышает допуска в 4% (фактически 0,36%).

            Поэтому окончательно выбираем   и

7.2.5 Определяем основные геометрические параметры зубчатой косозубой цилиндрической передачи  (№4).

- определим делительный диаметр шестерни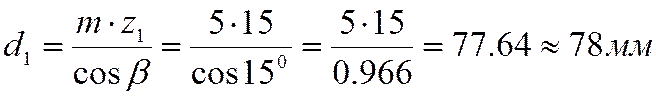

- определяем делительный диаметр колеса

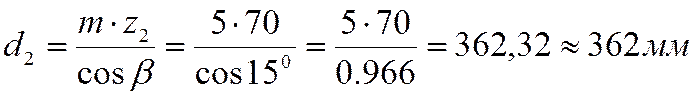
- определяем диаметры впадин зубьев:

шестерни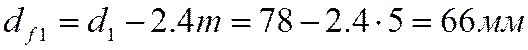

колеса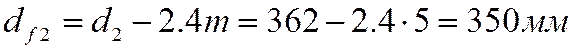      

- определяем диаметры вершин зубьев:

шестерни 

колеса        

- определяем ширину венца  зубьев:

колеса (из пункта 7.2.1 настоящего расчета )

шестерни

7.2.6  Определяем силы в косозубом зацеплении (№4 по кинематической схеме).

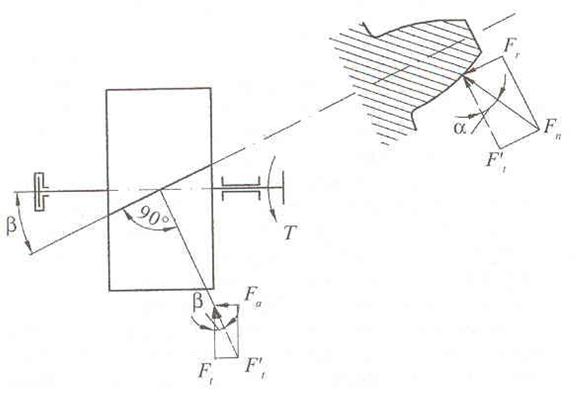
Согласно этой силовой схемы определим следущие силы:

- находим окружную силу в месте контакта зубьев шестерни и колеса 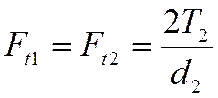, где 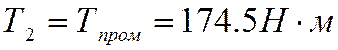  крутящий момент на промежуточном валу (на который насажено зубчатое колесо).   - делительный диаметр зубчатого колеса (пара №4 рис. 2.18).