|
|
|
Рис.4.2 |
Сравнение результатов.
Вычисляется погрешность определения реакции лишней связи по формуле
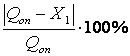
4.2. Лабораторная работа № 6 "Определение величины критической силы центрально сжатого стержня".
Цель опыта: экспериментальное изучение процесса потери устойчивости при осевом сжатии стержня большой гибкости и определение величины критической силы.
Испытанию подвергается стальной стержень прямоугольного поперечного сечения, шарнирно закрепленный на концах (m = 1).
Для исследования процесса потери устойчивости и определения критической силы стержень необходимо загружать постепенно возрастающей нагрузкой. На каждой ступени нагружения нужно аккуратно отклонить стержень от прямолинейного положения равновесия и отпустить его. Если стержень возвращается в исходное прямолинейное положение, то, значит, нагрузка не достигла критического значения. Если, после очередного увеличения нагрузки и отклонения стержня от прямоосного положения его кривизна возрастает, это значит, что сжимающая сила превысила критическую нагрузку и ее следует уменьшить. Величине критической силы соответствует нагрузка, при которой стержень находится в безразличном состоянии равновесия, то есть, будучи отклоненным от прямолинейного положения, останется искривленным, и кривизна его не будет ни убывать, ни возрастать.
Найденное из опыта критическое значение сжимающей силы записывается в журнал лабораторных работ. Кроме того, подсчитывается значение критического напряжения:
.
Теоретическое значение критической силы определяется по формуле Эйлера:
.
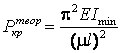Предварительно определяется гибкость стержня:
.
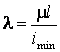Она должна быть больше λпред (для стали Ст.3, из которой сделан исследуемый стержень λпред = 100).
Теоретическое значение критического напряжения можно определить по формуле:
.
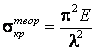В выводе сравнить экспериментальное и теоретическое значение критической силы.
4.2.1. Лабораторная работа № 7. "Ударная проба материала на излом"
Цель опыта: ознакомление с методикой испытания и оценка сопротивления материала динамическим нагрузкам при испытании на удар до разрушения.
Для оценки сопротивления материала излому ударом вводится новая механическая характеристика – ударная вязкость. Величина ударной вязкости определяется отношением количества энергии Т, затраченной на излом образца, к площади поперечного сечения образца в месте излома:
.
Испытание проводится на маятниковом копре. Принцип действия маятникового копра следующий. Маятник весом Q поднимается на некоторую высоту H0. При свободном падении маятник в самой нижней точке траектории движения разрушает образец и, продолжая движение, поднимается на высоту H1.
Кинетическая
энергия численно равна работе, затраченной на излом образца, измеряется
разностью величин энергии, которой обладал маятник до и после удара: 
, (силами сопротивления пренебрегаем).
Образец имеет форму бруска прямоугольного сечения. В средней части, там, где будет производиться удар, на образце делается надрез. Назначение его – вызвать в месте удара концентрацию напряжений и локализовать пластические деформации в малом объеме, то есть создать наиболее тяжелые условия для работы материала при динамическом воздействии.
Интересно познакомиться с
графиком зависимости величины ударной вязкости от температуры окружающей среды.
Оказывается, что в сравнительно узком интервале отрицательных температур
(примерно от 
до 
)
наблюдается резкое снижение ударной вязкости. С этим явлением связана так
называемая хладноломкость рельсов, бандажей и других деталей конструкции
подвижного состава.
Выводы: необходимо оценить применимость испытанного материала для строительных целей. При этом необходимо учитывать, что металл строительных конструкций должен иметь значение ударной вязкости не менее 100 Дж/см2.
5. КОНТРОЛЬНЫЕ ВОПРОСЫ К ЗАЧЕТУ И ЭКЗАМЕНУ[2]
Часть 2
Сложное сопротивление стержня
1. Понятие о сложном сопротивлении. Общий случаи действия сил на стержень большой жесткости (напряжение, нейтральная ось, проверка прочности).
2. Пространственный и косой изгибы (нормальные напряжения, нейтральная ось, условие прочности, перемещения).
3. Совместное действие на брус большой жесткости продольных осевых и поперечных внешних сил (нормальные напряжения, нейтральная ось, условие прочности).
4. Внецентренное растяжение-сжатие стержней большой жесткости (нормальные напряжения, нейтральная ось, условие прочности).
5. Совместные изгиб и кручение прямоосных стержней кругового поперечного сечения (нормальные и касательные напряжения, проверка прочности, эквивалентный момент, подбор сечений).
Энергетический метод определения упругих перемещений стержневых систем
6. Универсальная формула для определения перемещений в стержневых системах (интеграл Мора).
7. Графоаналитический прием вычисления интеграла Мора (прием Верещагина). Применение формулы Мора-Верещагина.
Метод сил для расчета статически неопределимых стержневых систем
8. Понятие о лишних связях, основной системе и условиях ее выбора. Каноническое уравнение. Расчет статически неопределимых балок методом сил.
Устойчивость центрально сжатого стержня*
9. Понятие о критической силе центрально сжатого стержня. Вывод формулы Эйлера.
10. Влияние способа закрепления стержня на величину критической силы. Приведенная длина. Гибкость сжатого стержня.
11. Критическое напряжение. Пределы применимости формулы Эйлера.
12. Устойчивость сжатого стержня за пределом упругости. Формула Ясинского. Полный график зависимости критического напряжения от гибкости сжатого стержня.
13. Условие устойчивости центрально сжатого стержня. Коэффициент понижения основного допускаемого напряжения. Особенности подбора сечений сжатых стержней по условию устойчивости.
14. Рациональные формы поперечных сечений сжатых стержней.
Динамические нагрузки*
15. Виды динамических нагрузок. Принцип Даламбера.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
