Сопротивление материалов. Часть 2: Учебное пособие для студентов заочной формы обучения, страница 6

Для вычисления осевого момента инерции  (прямоугольник – стенка) через центр второй фигуры проводится ось , совпадающая с осью . Осевой момент инерции  фигуры 2 равен  .

Окончательно получаем  .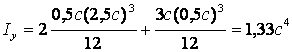

Осевые моменты сопротивления

   .

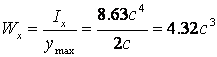
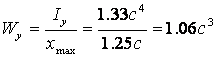3.  Подбор размеров поперечного сечения балки.

Условие прочности (3.1) переписывается в виде

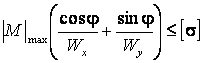                                         (3.7)

В соответствии с исходными данными принимается

  ,

,

Вычисленные значения  и  подставляются в формулу (3.7)

.

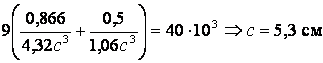Таким образом, подобраны размеры поперечного сечения заданной формы.

3.2.  Задача 7 "Внецентренное сжатие стержня большой изгибной жесткости"

На стержень заданного  поперечного сечения в точке D  действует сжимающая сила Р (рис.3.5)

Требуется:

1.  Вычертить в масштабе сечение стержня, показав положение главных центральных осей инерции.

2.  Определить положение нейтральной линии и показать ее на схеме сечения.

3.  Показать эпюру нормального напряжения и отметить в сечении положение опасных точек.

4.  Определить величину допускаемой нагрузки, приняв , .

Исходные данные приведены в таблице 1.

Таблица 1

Номер		b, см	с, см	а, см
строки	схемы (рис.3.5)
1	1	120	50	20
2	2	130	55	25
3	3	140	60	30
4	4	150	65	20
5	5	120	70	25
6	6	130	50	30
7	7	140	55	20
8	8	150	60	25
9	9	120	65	30
0	0	130	70	20
	А	В	А	В

Пример решения задачи.

Исходные данные приведены  на рис. 3.6,а

Величина допускаемой нагрузки  определяется из условия, что напряжение в наиболее нагруженной точке сечения достигает значения . В исходных данных задачи приведены два значения допускаемого напряжения, ‑  (допускаемое напряжение на растяжение) и  (допускаемое напряжение на сжатие). Это означает, что материал стержня по разному сопротивляется растяжению и сжатию (факт, характерный для хрупких материалов). При решении задачи вычисляются два значения допускаемой нагрузки:  - в предположении, что наибольшее растягивающее напряжение достигает значения  и  - в предположении, что наибольшее сжимающие напряжение достигает значения .

Из двух значений нагрузок ,  выбирается меньшая, для которой обеспечивается прочность материала по растягивающим и сжимающим напряжениям. Нормальные наибольшие растягивающие и  сжимающие напряжения возникают в точках, наиболее удаленных от нейтральной оси.

Рис.3.5

Уравнение нейтральной оси при внецентренном растяжении – сжатии имеет вид

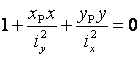,                                                  (3.8)

где

-   - координаты точки приложения силы Р,

-  х, у - координаты точек нейтральной оси,

-   - радиусы инерции поперечного сечения стержня.

Рис.3.6

Радиусы инерции вычисляются по формуле

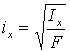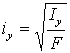,                                                 (3.9)

Для вычисления осевых моментов инерции  воспользуемся формулами (3.3) и (3.4)

                                                (3.10)

                                                (3.11)

На рис. 3.6,б исходное поперечное сечение представлено в виде трех прямоугольников.

Через центры фигур разбиения проводятся оси  и . Вычисляются собственные моменты инерции фигур ,

,   ,   ,  

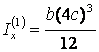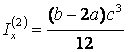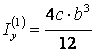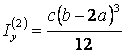
Совпадение осей  и x, а также  и означает, что координаты  и  центров фигур разбиения равны нулю.

Подстановка полученных результатов в формулы (3.3) и (3.4) дает

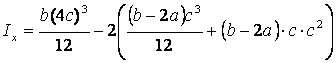                                   (3.12)

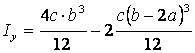                                                   (3.13)

Знак минус в формулах (3.12) и (3.13) связан с тем фактом, что фигуры разбиения 2 являются отверстиями. Подстановка в формулы (3.12) и (3.13) ,  и  дает , . Площадь F поперечного сечения стержня  или . Квадраты радиусов инерции поперечного сечения

, .

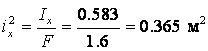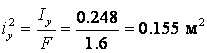Уравнение нейтральной оси (3.8) принимает вид

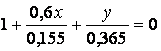                                                 (3.14)

Для построения нейтральной оси вычисляются координаты ее точек:

-  при      ,

-  при      .

Координаты (, ) и (, ) наносятся на чертеж сечения (рис.3.7), и через эти две точки проводится нейтральная ось.

К нейтральной оси проводится перпендикулярный отрезок а-а, на котором строится эпюра нормального напряжения . Через наиболее удаленные от нейтральной оси точки В и D проводятся параллельно нейтральной оси отрезки ВВ₁ и DD₁. Далее в произвольном масштабе откладывается отрезок D₁D₂, определяющий напряжение в точке D. Через точку D₂ и нулевую точку нейтральной оси проводится отрезок, определяющий положение точки В₂. Отрезок В₁В₂, в выбранном масштабе, соответствует напряжению . Таким образом, в точке D сечения реализуются наибольшие сжимающие, а в точке В наибольшие растягивающие напряжения.

Рис.3.7

Величина допускаемой нагрузки определяется из условия прочности для внецентренного растяжения – сжатия.

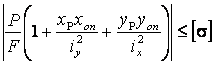,                                           (3.15)

откуда

Таким образом, грузоподъемность стержня  или

3.3.  Задача 8 "Статически неопределимые балки"

Двухпролетная балка с консолью, нагружена равномерно распределенной нагрузкой интенсивностью  q,  силой Р и парами сил m (рис. 3.8)

Требуется:

1.  Раскрыть статическую неопределимость задачи с помощью метода сил. Построить эпюру изгибающего момента.

2.  Подобрать поперечное сечение балки в виде двутавра, приняв [s] =160 МПа.

Исходные данные приведены в таблице 2.

Таблица 2