При нагрузках меньших критических, случайные малые воздействия не способны вызвать непроектную деформацию элементов.
Существует классификация состояний элементов:
при Р<Ркр- устойчивое,
при Р>Р кр –неустойчивое
при Р=Р кр -состояние безразличного равновесия сил , при котором наряду с проектной деформацией может иметь место и "непроектная" деформация элемента.
Критическая нагрузка Ркр для сжатых элементов определяется как наименьшая сжимающая сила, при которой наряду с прямолинейной формой равновесия становится возможной искривленная форма равновесия.
Величина критической силы для гибких стержней (λ>λпред) определяется по формуле Эйлера
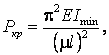(2.29)
где
- λ ‑ гибкость стержня,
- Imin –минимальный осевой момент инерции,
- μ –коэффициент приведения длины, зависящий от способа закрепления стержня (рис. 2.6)
|
|
|
Рис. 2.6 |
Гибкость
стержня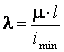 
, где 
‑
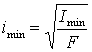минимальный радиус инерции.
Если стержень закреплен по-разному в двух плоскостях, необходимо определить два значения критической силы и выбрать меньшее.
Критическое напряжение σкр определяется по формуле:
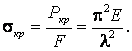(2.30)
Формула Эйлера
справедлива при 
, когда потеря устойчивости
происходит в области упругих деформаций, подчиняющихся закону Гука.
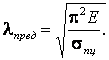(2.31)
Для
коротких стержней критическое напряжение sкр
принимается равным 
для хрупких
материалов и 
для пластичных материалов.
При
для определения критического
напряжения используется эмпирическая формула Ясинского 
Для малоуглеродистой стали a = 310 МПа, b = 1.14 МПа.
Для дерева a = 29.3 МПа, b = 0.194 МПа.
Для чугуна формула Ясинского выглядит следующим образом:
где a = 776 МПа,
b = 12 МПа, c = 0.053 МПа.
При расчете на прочность требовалось выполнение условия
Теперь
необходимо учитывать, чтобы 
не оказалось
больше 
.
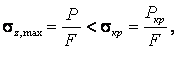
Для
обеспечения запаса устойчивости должно выполняться условие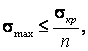 
где n
– коэффициент запаса по устойчивости, зависящий от возможного внецентренного
приложения сжимающей силы, от начальной кривизны оси стержня и т.д.
Если
обозначить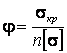 
(где φ– коэффициент снижения основного
допускаемого напряжения), условие устойчивости запишется в виде
,
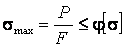(2.32)
значения φ зависят от гибкости λ и сведены в таблицу (приложение 3).
Задача проверки прочности и определения [P] для стержня с известными геометрическими характеристиками сечения не вызывают затруднений. Задача подбора сечения сжатых стержней более сложная. Дело в том, что коэффициент φ зависит от гибкости стержня, т. е. от формы и размеров поперечного сечения. В этом случае задача решается методом последовательных приближений (смотри пример решения задачи 9).
2.5. Динамическое действие нагрузки
Динамическая нагрузка – это нагрузка, быстро меняющая свое значение и местоположение (например, движущийся поезд). Важнейшим признаком динамического воздействия служит появление в элементах конструкций сил инерции, сопоставимых по величине с внешними воздействиями.
С силами инерции связаны дополнительные напряжения и деформации, которые могут превысить напряжения и деформации от статической нагрузки. В расчетах влияние динамических нагрузок учитывается динамическим коэффициентом.
Сначала динамическая нагрузка заменяется статической и от ее действия определяются напряжения и деформации, которые затем умножаются на динамический коэффициент.
Рассмотрим два случая динамического воздействия: расчет на прочность при движении тела с постоянным ускорением и приближенное решение задачи на удар.
2.5.1. Поступательное движение тела с постоянным ускорением.
Груз G поднимается с постоянным ускорением а (Рис. 2.7.а). Определим динамическое усилие, возникающее в тросе (весом троса пренебрегаем).
|
|
|
Рис.2.7 |
К телу, кроме веса, по принципу Даламбера, должна быть
приложена сила инерции 
, (где m – масса тела), направленная в сторону, противоположную
ускорению 
(Рис. 2.7.б). Тогда
,
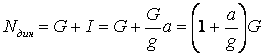где g – ускорение силы тяжести.
Динамический коэффициент при постоянном ускорении
.
Статическое усилие в тросе было бы Nст= G.
2.5.2. Ударное действие нагрузок.
Под ударом понимается взаимодействие движущихся тел в результате их соприкосновения, связанное с резким изменением скоростей движения точек этих тел за весьма малый промежуток времени.
Период соударения обычно очень мал и измеряется микро- или миллисекундами. Во время удара между соприкасающимися телами возникают весьма большие взаимные давления Рд. Эти силы вызывают напряжения в обоих телах. Таким образом, в ударяемом теле возникают такие напряжения, как будто к нему приложена сила инерции ударяющего тела. Мы могли бы их вычислить, рассматривая силу инерции Рд как статическую нагрузку. Затруднение заключается в определении этой силы инерции, так как мы не знаем продолжительности удара, то есть времени, за которое происходит изменение скорости. Значит, остается неизвестным ускорение.
Для вычисления Рд приходится использовать закон сохранения энергии.
Рассмотрим случай продольного упругого удара (рис.2.8.а).
При ударе кинетическая энергия Т ударяющего тела превращается в потенциальную энергию U упругой деформации ударяемого тела
.
|
|
|
Рис.2.8 |
Кинетическая энергия ударяемого тела может быть вычислена так
(2.33)
В основе теории удара лежит гипотеза о том, что эпюра перемещений системы от груза Q при ударе подобна эпюре перемещений, возникающих от того же груза при его статическом действии.Согласно этой гипотезе потенциальная энергия, накопленная в ударяемом теле, определится по формуле
(2.34)
Приравняем правые части формул (2.33) и (2.34)
Так
как 
(здесь 
–
деформация от статически приложенной силы Q, 
- динамический коэффициент), то
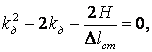
При внезапном приложении груза (Н=0) kд=2.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
