Сопротивление материалов. Часть 2: Учебное пособие для студентов заочной формы обучения, страница 7

Номер схемы (рис.3.8)	1	2	3	4	5	6	7	8	9	0	А
а,  м	6	7	8	9	10	11	12	10	8	6	В
q, кН/м	16	18	20	22	24	22	20	18	16	14	А
индекс	1	2	3	4	5	6	7	8	9	0

Пример решения задачи

На рис. 3.9,а показана один раз статически неопределимая балка. Примем в расчете , .

1.  Раскрытие статической неопределимости задачи.

Согласно алгоритму метода сил на первом шаге решения задачи производится выбор основной системы (рис.3.9,б). Основная система получается из заданной путем отбрасывания лишней связи (внешней или внутренней). В рассматриваемом примере в балку "врезается" шарнир над средней опорой.

Неизвестный опорный момент  определяется из канонического уравнения метода сил

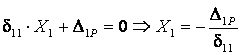                                          (3.16)

где

-   ‑ перемещение по направлению отброшенной связи, вызванное действием  

-   ‑ перемещение по направлению , вызванное действием заданной нагрузки

Рис.3.8

Рис.3.9

Вычисление перемещений  и  производится по формуле Симпсона:

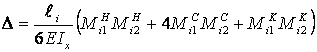                   (3.17)

где

-   - длина участка перемножения эпюр;

-   - ординаты первой эпюры изгибающего момента в начале, в конце и в середине участка ;

-  ,  ‑ ординаты второй эпюры изгибающего момента в начале, в конце и в середине участка  ;

Для вычисления коэффициентов канонического уравнения надо построить единичную и грузовую эпюры изгибающего момента.

Построение единичной эпюры производится в основной системе (рис. 3.9,б) в предположении . Очертание единичной эпюры изгибающего момента приведено на рис. 3.9,в.

При построении грузовой эпюры удобно расчленить исходную балку на две балки  и  (рис.3.9,г). Членение балки производится в месте постановки шарнира.

Балка  однопролетная, нагруженная равномерно распределенной нагрузкой интенсивностью . В силу симметрии реакции  и  одинаковые и равны . Балка  имеет один участок, поэтому для построения эпюры изгибающего момента достаточно рассмотреть равновесие одной отсеченной части (рис.3.9,д)

Эпюра  имеет параболическое очертание. В качестве третьей точки выбирается середина участка распределенной нагрузки, то есть

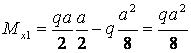
Очертание эпюры  в балке  приведено на рис.3.9,е.

Балка  однопролетная с консолью.

Для определения реакций опор записываются уравнения равновесия

.

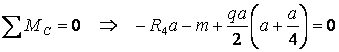
Для построения эпюры изгибающего момента в балке надо рассмотреть равновесие двух отсеченных частей (рис.3.9, д):

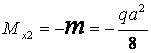 и ,

,

      ;           ;

   

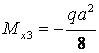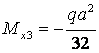
Очертание эпюры изгибающего момента в балке  приведено на рис.3.9,е.

Вычисление  и .

Коэффициент  вычисляется по формуле .

Единичная эпюра  имеет три участка (один нулевой), поэтому перемножение эпюры производится по двум участкам:

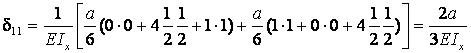
 вычисляется по формуле :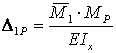

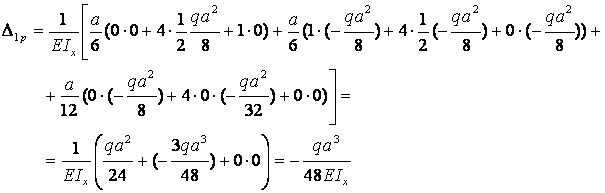
Вычисленные значения 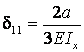 и 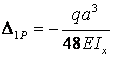 подставляются в каноническое уравнение (3.16)

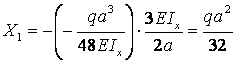
Ординаты эпюры изгибающего момента  в статически неопределимой балке вычисляются по формуле

                                        (3.18)

Эпюра изгибающего момента  представляет собой исходную единичную эпюру, ординаты которой увеличены в  раз (рис. 3.9,ж).

Если в расчете величина  получается отрицательной, то необходимо изменить знак эпюры  по отношению к эпюре .

Ординаты эпюры изгибающего момента  определяются суммированием соответствующих ординат эпюр  и  (таблица 3):

Таблица 3

Участки	Ординаты эпюр ()
Левый пролет:
Начало	0	0	0
Середина
Конец	0
Правый пролет:	-	-	-
Начало
Середина
Конец		0
Консоль:	-	-	-
Начало		0
Середина		0
Конец	0	0	0

Опасное сечение балки – середина первого пролета,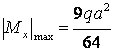

Подбор поперечного сечения

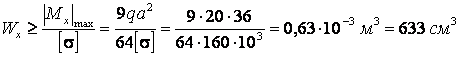
В сортаменте "Балки двутавровые"  (Приложение 1) в графе  берется значение, ближайшее к .

Оказывается, что такого значения в таблице нет. Ближайшими значениями осевого момента сопротивления являются:

 и . Сначала берется ближайшее меньшее значение  и определяется величина напряжения в материале балки

.

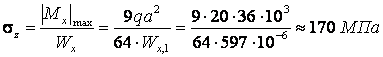Затем определяется перенапряжение

.

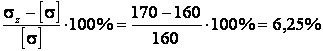Так как перенапряжение больше 5%, то принимается двутавр № 36 ().

3.4.  Задача 9 "Устойчивость центрально – сжатого стержня"

Стойка двутаврового поперечного сечения одинаково закреплена в обеих главных центральных плоскостях инерции поперечного сечения и центрально сжата силой Р (рис.3.10,а)

Требуется:

1.  Определить грузоподъемность  стержня.

2.  Для найденного значения грузоподъемности с целью экономии материала заменить двутавр на более рациональное сечение (два двутавра или два швеллера, соединенных планками на сварке (рис.3.10,б). Подобрать площадь нового сечения и сравнить с площадью первоначального сечения.

Исходные данные приведены в таблице 4.

Таблица 4

Номер строки	Расчетная схемы стойки (рис.3.10,а)	l, м	Номер двутавра	Схема для подбора нового варианта сечения (3.10,б)
1	1	2,6	27	1
2	2	2,8	30	2
3	3	3,0	33	3
4	4	3,2	36	2
5	1	3,4	40	1
6	2	3,6	45	2
7	3	3,8	27	3
8	4	4,0	30	1
9	1	4,2	50	2
0	2	4,4	55	3
	А	В	А	В