Сопротивление материалов. Часть 2: Учебное пособие для студентов заочной формы обучения, страница 8

Пример решения задачи

Исходные данные приведены на рис. 3.11.

1.  Определение грузоподъемности стержня.

Грузоподъемность центрально сжатого стержня определяется по формуле

,                                        (3.19)

где  – коэффициент понижения основного допускаемого напряжения.

Коэффициент  зависит от , то есть . Гибкость вычисляется по формуле

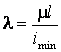,                                                   (3.20)

где

-  μ - коэффициент приведения длины стержня,

-   ‑ минимальный радиус инерции поперечного сечения стержня

Величина  определяется по сортаменту "Балки двутавровые" (Приложение 1). Для заданного номера двутавра № 36 в сортаменте находим , , следовательно . При шарнирном опирании стержня коэффициент приведения длины .

Гибкость стержня .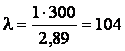

а)
б)
Рис.3.10

Рис.3.11

По таблице коэффициента продольного изгиба (Приложение 3) для  и стали марки Ст. 4, 3, 2 определяется значение коэффициента  понижения основного допускаемого напряжения. В таблице зависимости  от  значения гибкости кратны 10. Поэтому, из таблицы берутся два ближайших к найденному значения гибкости  и соответствующие им два значения :

,  

,   .

Для определения искомого значения коэффициента  выполняется линейная интерполяция:

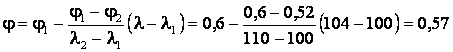
Величина допускаемой нагрузки на устойчивость

где

-   см² ‑ площадь поперечного сечения двутавра № 36 (берется по сортаменту).

2.  Подбор рационального поперечного сечения стержня.

Рациональным поперечным сечением является сечение, у которого главные моменты инерции одинаковые . У стандартных прокатных профилей моменты инерции  и  значительно отличаются (например, для двутавра I № 36 , ). В расчетах на устойчивость используется минимальный момент инерции . Максимальный момент инерции , не используемый в расчетах на устойчивость, косвенно свидетельствует о наличии перерасхода материала.

Рациональное поперечное сечение может быть сконструировано с помощью двух одинаковых прокатных профилей. (рис. 3.11,б). Варьируя значение величины а (или с), можно для любого номера швеллера добиться выполнения условия  . Момент инерции  двух швеллеров равен  ( - осевой момент инерции швеллера, определяется по номеру швеллера).

При подборе рационального поперечного сечения стержня, определенная ранее величина допускаемой нагрузки , принимается в качестве исходной

Формула (3.19) переписывается в виде

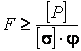                                                    (3.21)

В правую часть формулы (3.21) входит коэффициент , который зависит от площади , так как , а 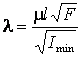. Такие уравнения решаются методом последовательных приближений.

На первом шаге назначается среднее значение коэффициента . Подстановка  в формулу (3.21) дает величину требуемой площади поперечного сечения .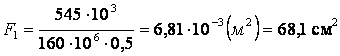

Площадь одного швеллера

По сортаменту "Швеллеры" (Приложение 2) по величине  подбирается номер прокатного профиля, площадь поперечного сечения которого , это швеллер [ № 27 (, ).

Осевые моменты инерции рационального поперечного сечения одинаковые . Вычисляется минимальный радиус инерции рационального сечения

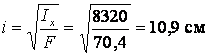
Определяется гибкость стержня

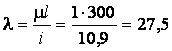
По таблице "Коэффициент продольного изгиба " (Приложение 3) для  и материала Ст. 4, 3, 2 находится . Допускаемые напряжения на устойчивость .

Вычисляются нормальные напряжения

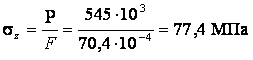
Эти напряжения сравниваются с . Недонапряжение составляет

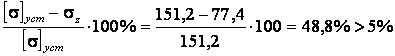
Необходимо продолжить подбор.

В начале второго шага приближения выбираем

,

затем из (3.21) определяем площадь, выбираем швеллер, определяем гибкость стержня, определяем , вычисляем  и , проверяем выполнение условия

.

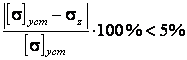Если оно верно, то подбор сечения закончен, если нет – необходимо переходить к следующему шагу приближения, который выполняется аналогично.

В данном примере необходимо сделать четыре шага приближения. В результате выбираем швеллер № 16   (,). В этом случае

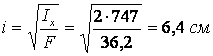
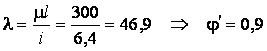
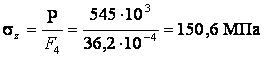
Перенапряжение . Так как величина перенапряжения составляет менее , то расчет можно считать выполненным.

Таким образом, выбрано рациональное сечение стержня в виде двух швеллеров № 16.

За счет рационального проектирования поперечного сечения стержня достигнут экономический эффект, который может быть оценен путем сравнения начальной площади  поперечного сечения и конечной :

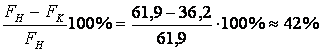
Для определения линейного размера c (рис. 3.11, б) составляется выражение осевого момента инерции рационального сечения стержня относительно оси y

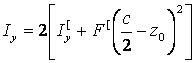
Так как

,

то

,

В результате решения данного квадратного уравнения определяется значение .

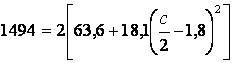
Таким образом, выполнены расчет и проектирование рационального поперечного сечения центрально сжатого стержня.

4.  ЛАБОРАТОРНЫЙ ПРАКТИКУМ

4.1.  Лабораторная работа №5. "Определение реакции лишней связи в статически неопределимой балке"

Цель опыта: сравнение теоретической и опытной величин реакции лишней связи.

Постановка опыта.

Рис.4.1

Методика проведения опыта.

После ознакомления с опытной установкой в журнал наблюдений записываются величины l, c, P. Фиксируется начальный отсчет  прибора (рис.4.1). К балке прикладывается груз P заданной величины. Под действием груза P происходит искривление оси балки, что приводит к изменению показания прибора. С помощью коромысла к балке прикладывается второй груз Q. Варьированием величины груза Q можно изменять показания прибора. В опыте требуется подобрать такую величину  груза, при котором прибор будет показывать начальный отсчет . Найденное значение  соответствует искомой величине реакции лишней связи.

Теоретический расчет.

Реакция  лишней связи определяется из канонического уравнения метода сил

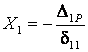
Коэффициенты  и  определяются по формуле Симпсона

Ординаты определяются с помощью грузовой и единичной эпюр изгибающего момента (рис.4.2).