Сопротивление материалов. Часть 2: Учебное пособие для студентов заочной формы обучения, страница 3

После определения начального угла поворота  вычисляется прогиб сечения А.

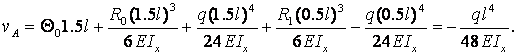
Примечание. Распределенная нагрузка q, показанная на рис.2.3 пунктиром, вводится  в тех случаях, когда прогиб определяется в сечении, которое находится за пределами участка действия распределенной нагрузки.

Угол поворота сечения В вычисляется по формуле (2.20), в которой следует принять

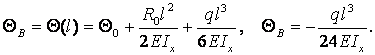
2.2.2.  Интеграл Мора.

Универсальная формула Мора вычисления упругих перемещений в стержневых системах является естественным обобщением формулы Кастильяно. Для линейно упругих стержневых систем формула Кастильяно имеет вид

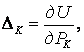                                                (2.21)

где

Δ_К  -обобщенное перемещение сечения К,

Р_К –обобщенная сила, соответствующая обобщенному перемещению Δ_К,

U –функция потенциальной энергии.

Потенциальная энергия является квадратичной функцией усилий и для изгибаемых элементов записывается в виде

                                (2.22)

В подавляющем большинстве случаев влиянием поперечной силы  на величину потенциальной энергии пренебрегают. Комбинирование формул (2.21) и (2.22) дает

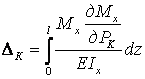                                           (2.23)

Частная производная  соответствует функции изгибающего момента , вызванного действием единичной обобщенной силы ,приложенной в сечении К по направлению искомого перемещения. Формула (2.23), записанная в виде

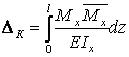                                         (2.24)

определяет частный вид универсальной формулы Мора применительно к определению перемещений в изгибаемых элементах.

На практике используется графоаналитический прием вычисления интеграла Мора (прием Верещагина).

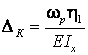,                                                (2.25)

где

 ‑ площадь грузовой эпюры (эпюра изгибающего момента от действия заданной нагрузки);

 ‑ ордината единичной эпюры (эпюра изгибающего момента от действия единичной обобщенной силы), измеренная под центром грузовой эпюры.

Вычисление интеграла Мора по формуле Верещагина в учебной литературе называется "перемножением" эпюр.

В ряде случаев при вычислении интеграла Мора удобно пользоваться формулой Симпсона

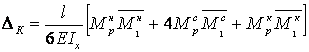                    (2.26)

где индексы "н", "с", "к"  ‑ обозначают соответственно начало, середину и конец участка перемножаемых эпюр.

Пример 2. Определить прогиб сечения А и угол поворота сечения В  балки, рассмотренной в примере 1 (рис.2.4.а).

Вычисление интеграла Мора произвести по формуле Симпсона.

Для определения прогиба сечения А строится грузовая М_р  (рис.2.4.б) и единичная (рис.2.4.в) эпюры изгибающих моментов.

Перемножение  грузовой  и единичной  эпюр изгибающих моментов по формуле Симпсона дает

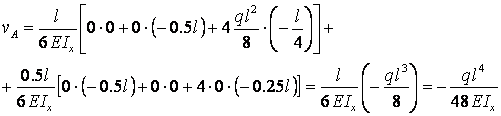
Для определения угла поворота опорного сечения  В строится вторая единичная эпюра изгибающего момента от действия единичного момента, приложенного в сечении В  балки (рис.2.4.г).

Рис.2.4

Величина угла поворота  определяется перемножением грузовой  и единичной  (рис.2.4.г) эпюр изгибающих моментов.

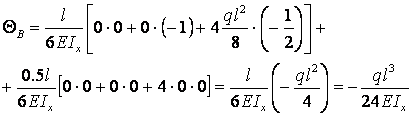
Примечание. Знак минус в ответах означает, что направления действительных перемещений сечений А и В  будут противоположными направлениям перемещений, соответствующих единичным обобщенным силам.

2.3.  Статически неопределимые балки
(Метод сил раскрытия статической неопределимости)

Статически неопределимые балки содержат "лишние" связи (при удалении лишних связей балки становятся статически определимыми). Число лишних связей определяет степень статической неопределимости задачи.

Статически определимая геометрически неизменяемая балка, полученная из заданной статически неопределимой путем удаления лишних связей, называется основной системой метода сил.

Алгоритм решения статически неопределимых балок методом сил рассмотрен на примере один раз статически неопределимой балки (рис. 2.5.а).

Решение задачи начинается с выбора основной системы метода сил (рис. 2.5.б). Следует отметить, что это не единственный вариант выбора основной системы (в частности, возможен вариант удаления внутренних связей путем постановки шарнира).

Суть метода сил заключается в отрицании перемещений по направлению удаленной связи. Математически это условие записывается в виде уравнения совместности перемещений

,                                                (2.27)

где

δ₁₁ – перемещение по направлению отброшенной связи, вызванное действием единичного значения неизвестной реакции удаленной связи  (рис. 2.5.в)

Δ_1Р – перемещение по направлению отброшенной связи, вызванное действием заданной нагрузки (рис. 2.5.г)

Вычисление перемещений δ₁₁,  Δ_1Р  производится по формуле Симпсона.

Коэффициент δ₁₁  канонического уравнения метода сил  определяется перемножением единичной эпюры  (рис. 2.5.е) самой на себя

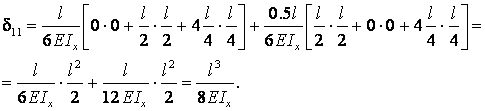
Рис. 2.5

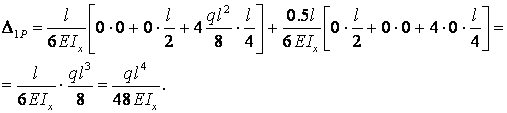
Коэффициент Δ_1Р канонического уравнения метода сил  вычисляется перемножением единичной  (рис. 2.5.е) и грузовой  (рис. 2.5.д) эпюр

Из решения уравнения (2.27)  определяется реакция X₁  лишней связи

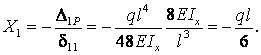
Этот этап решения соответствует раскрытию статической неопределимости задачи.

Эпюра изгибающего момента М_x (рис. 2.5.з) в статически неопределимой балке строится по формуле

                                      (2.28)

На рис. 2.5.ж представлена "исправленная" единичная эпюра, все ординаты которой увеличены в  X₁  раз.

Рассмотренный алгоритм решения статически неопределимых задач с помощью метода сил пригоден и для решения статически неопределимых задач при кручении, при осевом действии нагрузок, а также при сложной деформации стержня.

2.4.  Устойчивость сжатых стержней

Для полного представления о работе сооружения наряду с расчетами на прочность и жесткость необходимы расчеты на устойчивость сжатых и сжато-изогнутых элементов.

Инженерные объекты кроме расчетных нагрузок могут подвергаться дополнительным, не предусмотренным в расчете, малым возмущениям, способным вызвать в элементах объекта непроектную деформацию (искривление оси сжатых элементов, пространственный изгиб плоско изогнутого элемента). Результат такого дополнительного воздействия зависит от  интенсивности нагрузок, действующих на элемент конструкции. Для каждого элемента существует некоторое критическое значение нагрузки, при  превышении которого малое случайное возмущение вызывает необратимую непроектную деформацию. Такое состояние  объекта является опасным.