Сопротивление материалов. Часть 2: Учебное пособие для студентов заочной формы обучения, страница 5

В случае поперечного удара коэффициент динамики вычисляется по  аналогичной формуле 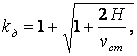где v_ст  - статический прогиб балки в месте падения груза, вызванный действием силы, равной весу падающего груза.

3.  ЗАДАНИЯ НА КОНТРОЛЬНЫЕ РАБОТЫ С ПРИМЕРАМИ РЕШЕНИЯ.

Содержание контрольных работ

№ контрольной работы	Семестр	Раздел	Специальности
			МТ, СЖД	ЛТ,В, ПТМ, ЭТ	ЭУС, УПП	ВиВ, ПГС
			номера задач
1	IV	I	1,3	1,3	2,3	1,3
2	IV	I	4,5	4,5	7,9	4,5
3	V	II	6,7	6,7		6,7
4	V	II	8,9	8,9		8,9

Вариантом являются два числа А и В. Эти числа студенты берут в зависимости от номера зачетной книжки. Причем А – последняя цифра номера, В – предпоследняя. Например, номеру зачетной книжки 99-ЛТ-35 соответствует  вариант А=5, В=3.

3.1.  Задача 6 "Косой изгиб стержня"

Консольная балка  нагружена равномерно распределенной нагрузкой q, сосредоточенной силой Р и моментом  (рис.3.1).

Поперечное сечение балки приведено на рис.3.2 (уголопределяет плоскость действия нагрузки на балку).

Требуется:

1.  Вычертить в масштабе схемы балки и поперечного сечения.

2.  Построить эпюру изгибающего момента (эпюру обязательно расположить под схемой балки).

3.  Вычислить осевые моменты сопротивления ,   поперечного сечения балки.

4.  Подобрать размеры поперечного сечения балки, приняв ,

Исходные данные приведены в таблице.

Таблица.

Номер схемы (рис.3.1)	1	2	3	4	5	6	7	8	9	0	А
Номер схемы (рис.3.2)	1	2	3	4	5	6	7	8	9	0	B
a, м	1,2	1,4	1,6	1,8	2,0	2,2	2,0	1,7	1,4	1,1	A
q, кН/м	14	12	10	8	6	4	7	10	13	16	B
индекс	1	2	3	4	5	6	7	8	9	0

Рис.3.1

Рис.3.2

Пример решения задачи.

Исходные данные задачи приведены на рис.3.3,а и рис.3.4,а. Примем в расчете .

Подбор поперечного сечения балки при косом изгибе производится с помощью условия прочности

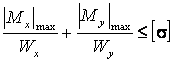,                                        (3.1)

где

-  , - составляющие вектора изгибающего момента М, возникающего в плоскости действия нагрузки,

-  - угол, образованный вектором нагрузки с вертикальной осью симметрии у.

Для определения максимального изгибающего момента  строится эпюра изгибающего момента в плоскости действия нагрузки.

1.  Построение эпюр усилий. 

В консольных балках эпюры усилий можно строить без предварительного вычисления реакций в заделке. Но в этом случае, очевидно, необходимо рассматривать равновесие отсеченной части, не содержащей опоры. Этот прием использован при решении данной задачи (методика построения эпюр усилий в балках изложена в примере решения задачи 5).

Балка содержит два участка длиной а=3м каждый. В произвольном месте первого участка проводится сечение 1 и рассматривается равновесие правой отсеченной части (рис.3.3,б) Длина отсеченной части переменная величина . В сечении 1 показываются положительные усилия  и . Записываются уравнения равновесия для отсеченной части

,

.

Рис.3.3

Аналогично, в произвольном месте второго участка балки проводится сечение 2 и рассматривается равновесие правой отсеченной части (рис. 3.3,в) Длина отсеченной части переменная величина . В сечении 2 показываются положительные усилия , . Составляются уравнения равновесия отсеченной части.

.

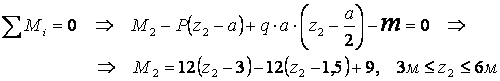
По вычисленным значениям Q и M строятся эпюры усилий (рис.3.3,г,д).

Таким, образом, максимальный изгибающий момент в балке .

2.  Вычисление осевых моментов сопротивления

Осевые моменты сопротивления   вычисляются по формулам

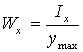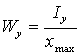, ,                                           (3.2)

где

-   – осевые моменты инерции поперечного сечения

-  - координаты наиболее удаленных точек сечения

Осевые моменты инерции  вычисляются по формулам

                                           (3.3)

                                          (3.4)

где

-  i – индекс, обозначающий число фигур разбиения составного сечения,

-   ,  – осевые моменты инерции  – ой фигуры разбиения относительно собственных центральных осей

-  - координаты центра  – ой фигуры разбиения относительно осей .

Заданное сечение балки (рис.3.4,а) состоит из трех прямоугольников (рис.3.4.,б), - двух полок 1 и стенки 2. Полки 1 расположены симметрично относительно осей , поэтому вычисления выполняются для одной полки, а результат вычислений удваивается. Формулы (3.3) и (3.4) принимают вид

                              (3.5)

                              (3.6)

Для вычисления момента инерции  через центр полки проводится ось , параллельно оси x. Осевой момент инерции прямоугольника 1 относительно оси  равен . Расстояние между осями , x определяет ординату . Площадь .

Для вычисления момента инерции  через центр второй фигуры разбиения (прямоугольник - стенка) проводится ось , совпадающая с осью x, следовательно . Момент инерции . Окончательно получаем

.

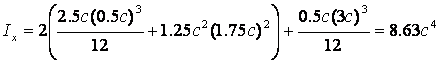Рис.3.4

Для вычисления осевого момента инерции  через центр первой фигуры разбиения (прямоугольник – полка) проводится ось , совпадающая с осью  (тогда ). Момент инерции прямоугольника – полки 1 относительно оси   равен .