Место и роль ЭСПУ станками, промышленными роботами, программируемых контроллеров, их задачи и функции, страница 5

Интерполяцию выполняют с помощью электронных схем (в УЧПУ Н22,Н33) либо с помощью ПО (в микропроцессорных УЧПУ). Однако в обоих случаях интерполируют по одним и тем же математическим выражениям.

Интерполятор отрабатывает программу последовательно отдельными участками (кадрами). При линейной интерполяции это участки прямых линий, расположенных в пространстве. Предположим, что необходимо отработать кадр, представляющий собой отрезок АВ, расположенный в плоскости ХУ.

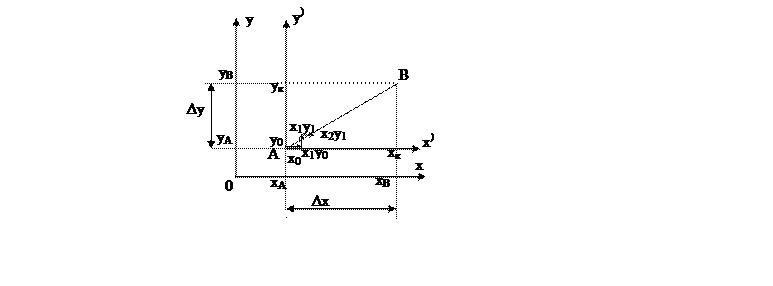
т.А (х_А,у_А), т.В (х_В,у_В). Отработку кадра ведут от т.А к т.В. Особенностью интерполяции является то, что исходной информацией для него является не координаты точек, а разность координат между конечной т. В и начальной т. А, т.е. Δх=х_В-х_А, Δу=у_В-у_А. В микропроцессорных УЧПУ эта разность вычисляется, а в УЧПУ со схемной реализацией алгоритмов задается при программировании.  Это равносильно тому, что для каждого отдельного участка устанавливают свою относительную систему координат (х⁾,у⁾), при этом начало относительной системы координат совпадает с началом отрабатываемого отрезка, т.е. х₀⁾=0, у₀⁾=0, х_К⁾= Δх, у_К⁾= Δу.

На каждый импульс, вырабатываемый интерполятором, привод подач соответствующей координаты станка осуществляет единичное перемещение в соответствии с дискретностью станка. Например, при перемещении на 5 мм и дискретности 0.01мм интерполятор должен выдать по этой координате 500 импульсов.

Кадр программы: N1 G01 X+7625. Y-4300. Z+0710 LF. Интерполятор этот кадр обрабатывает за определенное время, в соответствии со скоростью подачи, задаваемой от программы в блок задания скорости. Для того чтобы рабочий орган станка перемещался строго вдоль запрограммируемого отрезка прямой, импульсы, вырабатываемые интерполятором по каждой из координат, должны быть равномерно распределены по времени. Неравномерность следования импульсов определяет точность интерполятора и влияет на работу приводов подачи.

Линейная интерполяция методом оценочных функций.

Интерполируемая прямая АВ разделяет плоскость ХУ на 2 области: F>0 – где значение оценочной функции положительное число и F<0 – где значение оценочной функции отрицательное число. Область F>0 находится над прямой, F<0 – под прямой, интерполируемый отрезок АВ представляет собой область, где F=0.

Если промежуточная точка траектории интерполяции находится в области F>0, то следующий шаг по оси Х. Если же промежуточная точка траектории находится в области F<0, то следующий шаг по оси У. Поскольку работа происходит в относительной системе координат, начало интерполируемого отрезка всегда находится в начале координат. При этом начальная точка траектории интерполяции находится в области F=0 и первый шаг делается по оси Х. Шаги делаются непрерывно, с частотой задаваемой блоком задания скорости, до тех пор пока не достигнем конечной точки. Величина и знак оценочной функции вычисляется интерполятором. Для каждой промежуточной точки x_iy_j оценочная функция F_ij зависит от конечных координат и вычисляемых текущих координат  F_ij=y_jx_k-x_iy_k. F₀₀=0.

Текущее значение оценочной функции определяется следующим образом:

При шаге по оси Х координата у текущей точки не изменяется, а координата х увеличивается на 1, т.е. х_i+1=x_i+1. При шаге по оси У -  у_j+1=у_j+1.

При шаге по оси Х из т.(x_iy_j) в т.(x_i+1y_j) оценочная функция F_i+1j=y_jx_k-x_i+1y_k= y_jx_k-( x_i+1)y_k=

=y_jx_k- x_iy_k- y_k= F_ij- y_k. Знак оценочной функции определяет направление следующего шага.

Круговая интерполяция методом оценочных функций.

Окружность, на которой расположен интерполируемый отрезок, разделяет плоскость ХУ на 2 области: F>0 и F<0 (внутри). Интерполируемый отрезок дуги имеет начальную точку х₀у₀ и конечную х_Ку_К.

Если промежуточная точка находится в области F>0, то следующий шаг делается по оси Х.

Если промежуточная точка находится в области F<0, то следующий шаг делается по оси У.