Конспект лекций по дисциплине «Устройство и эксплуатация железнодорожного пути», страница 9

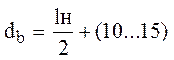
Расчет основных и осевых размеров стрелочного перевода

Определение основных геометрических размеров стрелочного перевода производят путем проектирования всех элементов стрелочного перевода на осях, параллельных и перпендикулярных продольной оси железнодорожного пути. Уравнение проекций всех элементов стрелочных переводов (для перевода с прямыми остряками) на указанные оси имеют вид (рис.4.13):

l_oCosβ+R¹_o[Sinα-Sinβ] +K¹Cosβ+KCosα=Z_m

l_oSinβ+R¹_o[Cosβ-Cosα]+K¹Sinβ+KSinα=S

Полная (практическая) длина стрелочного перевода равна

Z_o=Z_m+q₁+m

Осевые размеры стрелочного перевода определяют по зависимостям

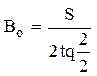
а_о=Z_m-b_o

a-=a_o+q₁

b=b_o+m

В приведенных выше зависимостях:

Z_n- практическая (полная) длина стрелочного перевода;

Z_m- теоретическая длина стрелочного перевода;

К – длина прямой вставки перед математическим центром крестовины;

К¹- длина прямой вставки за корнем прямого остряка;

R – радиус переводной кривой;

а – расстояние от начала рамных рельсов до центра стрелочного перевода;

а_о- расстояние от начала остряка до центра стрелочного перевода;

в – расстояние от центра перевода до конца крестовины;

в_о- расстояние от центра перевода до математического центра крестовины.

1.4. Построение эпюры стрелочного перевода

После окончания расчета всех геометрических размеров стрелочного перевода, необходимо приступить к построению эпюры стрелочного перевода.

Эпюра строится в масштабе 1/50 или 1/100.

На чертеже должны быть указаны основные линейные и угловые размеры (заданные или полученные расчетом) стрелочного перевода. Пример чертежа эпюры стрелочного перевода (см. рис. 4.10).

На чертеже должны быть приведены ведомости длин рубок, применяемых для укладки перевода.

1.1.  Расположение смежных стрелочных переводов

1.1.1.  Расстояние между центрами стрелочных переводов расположенных на прямом пути.

В зависимости от схемы расположения переводов (рис.4.4.) расстояние между их центрами определяется уравнениями, приведенными в табл.4.1.

Таблица 4.1.

№№	Наименьшее расстояние между центрами стрелочных переводов	Прямая вставка «d» в м. на путях
		Главных и приемо-отправочных		Прочих станционных и внутренних
		в нор.условиях	В стесн. условиях и при переуст. путей при однотипн. переводах	В норм. условиях	В стесненных условиях при однотипн. переводах

1. l = α₁+ d +α₂            12,5                 6,25                  3,125                0

2. l =α₁ +d+α₂               12,5                6,25                  3,125                0

6,25              3,125                3,125                0

Для всех условий

3. l = b₁+k₁+d + d₂        d≥ 3,125 при К ‹ 3,125; d = 0 при К₁›3,125

4. l = b₁+К₁ +d  +К₂ +b₂   d= S -(b₁+ К₁ + К₂+b₂) Sin α

Но не менее 3,125

5. l = α₁+ d + K₂ + b₂                   d = S       -(d₁ +K₂+b₂) Sinα

Но не менее 3,125

α₁; α₂ – расстояние от переднего стыка рамного рельса до центра соответствующего перевода;

b₁;b₂ – расстояние от центра перевода до хвостовика соответствующей крестовины,

К₁; К₂ – расстояние от хвостовика крестовины до ближайшего стыка;

d – прямая вставка или рубка;

l – расстояние между центрами смежных переводов.

1.5.2. Расстояние между стрелочным переводом и началом кривой

Расстояние до начала кривой определяется по зависимости

l_k =a + d

где d –прямая  вставка, перед кривой величина которой приведена в табл.4.2.

Таблица 4.2.

Схема	Радиус кривой	Длина прямой вставки «d»  м
		в нормальных условиях	в стесненных условиях при переустр. путей

3.2.а                 Более 250                                   6                               4

150 250                                   8                                6

Менее 150                                   12                              8