Анализ точности электронных средств. Работы по вероятностно-статистическим методам анализа, страница 8

Среди N₂ возможных ситуаций устройства при матричных испытаниях будет обнаружено некоторое количество Q отказных ситуаций с точки зрения заданного критерия отказа рассматриваемого устройства. Отказные ситуации будем отмечать чертой сверху. Они могут быть определены натурным физическим моделированием, поскольку такое моделирование позволяет довольно точно воспроизвести работу устройства и автоматически учесть все факторы, влияющие на его работоспособность, в том числе и второстепенные, которые при всех других видах моделирования, как правило, не учитываются.

Результаты матричных испытаний позволяют найти область работоспособности устройства (рис. 2), вероятность нахождения выходного параметра в пределах поля допуска и оптимизировать работоспособность.

 

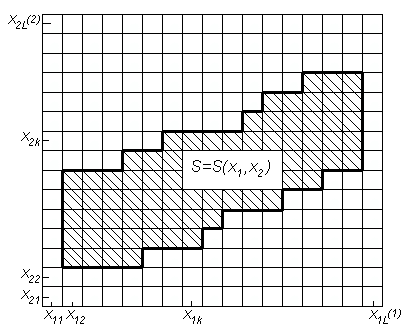
Рис. 2.  Область работоспособности

Вероятность того, что схема окажется неработоспособной, выразится так:

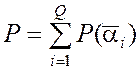, где Q  – число отказных ситуаций.

Вероятность отказных ситуаций, если определяющие первичные параметры независимы, находят как произведение вероятностей нахождения параметров в соответствующих квантах. Например, для ситуации a₁

.

Вероятность нахождения параметров X₁ и X₂ в квантах x11 и x₂₁ можно вычислить, если известны законы распределения f(x) этих параметров, по выражению

.

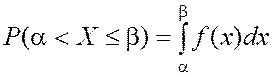Вероятность будет численно равна площади фигуры под кривой распределения, построенной на основании, равном длине кванта (рис. 3).    При нормальном законе распределения эти вероятности могут быть найдены по формуле

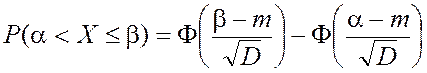, где  Ф(z) – функция Лапласа (из таблицы П1);  a, b – границы кванта;       m, D  – математическое ожидание и дисперсия соответственно.

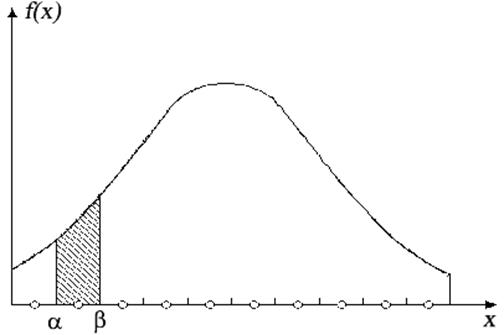
Рис. 3.  Плотность распределения параметра X

Для сравнительной оценки вероятность работоспособности исследуемого устройства может быть найдена по формуле

.

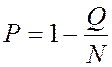Вероятность здесь будет несколько заниженной из-за принятия веса каждой отказной ситуации, равной единице. Если в некоторый фиксированный момент времени t известна плотность распределения параметров X₁ и X₂, то задача оптимизации работоспособности исследуемого устройства для этого момента времени геометрически может рассматриваться как задача отыскания такого положения функции f(x₁, x₂), чтобы объем, вырезаемый из f(x₁, x₂), восстановленный цилиндром с основанием S(x₁, x₂), был бы максимальным. Аналитически это записывается в ви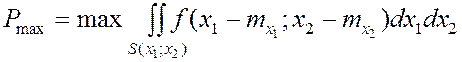де

, где  ,  – математическое ожидание функции f(x₁, x₂);

Р_max  – максимальная вероятность нахождения выходного параметра в пределах поля допуска.

Практически задача оптимизации может быть сведена к расчету новых номинальных значений определяющих первичных параметров [1].

Эти значения могут быть установлены простой процедурой нахождения координат центра тяжести n-мерной области работоспособности       (в рассматриваемом случае – двумерной области) исследуемого устройства. Координата центра тяжести по j-му параметру x_jl :

, где N  – общее количество ситуаций;  Q  – количество отказных ситуаций; Q_{j , c+1}  – количество отказных ситуаций, соответствующих c+1 кванту.

Достоинства метода матричных испытаний – возможность количественной оценки работоспособности. Недостатки – значительная трудоемкость и сложность использования для устройств, в которых моделирование первичных параметров затруднено.

Описание экспериментальной установки

Принципиальная схема УНЧ представлена на рис.4. Он усиливает синусоидальное  напряжение в диапазоне 50 Гц – 50 кГц.

Отказом считается уход коэффициента усиления К за пределы поля допуска. Наибольшее влияние на К оказывают сопротивление нагрузки в цепи коллектора R3, сопротивление автоматического смещения в цепи эмиттера R4, которое особенно критично [1], напряжение источника питания.

Для матричных испытаний устройство смонтировано в виде макета, установленного в термошкафу. При помощи галетных переключателей, рукоятки которых выведены на внешнюю сторону дверцы термошкафа, можно устанавливать различные значения параметров резисторов R3 и R4.